Two types of diffusions are used to control nonlinear instability and aliasing.
The second-order diffusion is used for temperature and moisture equations with
diffusion coefficients viscT and viscQ, respectively.
A more scale-selective fourth-oder diffusion is used in the momentum
equations with a tunable diffusion parameter visc4U.
The second-order diffusion scheme takes the form
and center differencing is used for 
.
The fourth-order diffusion is of the form
and a nine-point differencing is used following the scheme used in the
PSU/NCAR MM5. With an isotropic x and y coefficients, and absorbing a
factor of (grid space) 
, this is
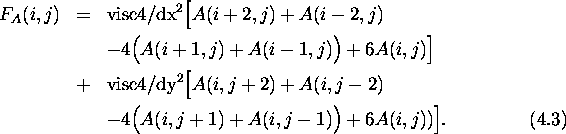
The nine points used (labeled by their weights) for this scheme are as follows (for the diffusion on the center point).
0 0 1 0 0
0 0 -4 0 0
1 -4 6 -4 1
0 0 -4 0 0
0 0 1 0 0
In version 2.3, spherical geometry is considered for the differential
equations. In horizontal diffusion schemes, the weights for the
points in the difference stencil satisfy
for
any field A, and
when cos(j)=1, the
weights are the same as in Cartisian Coordinate shown above.
The use of the fourth-order diffusion scheme was originally motivated by the desire to have diffusion terms be negligible in the zonal and vertical average momentum budget (relative to the balance of surface stress and nonlinear momentum transport). Downgradient diffusion is a poorer approximation for momentum than for a conserved tracers, hence the decision to try and keep the impacts of horizontal diffusion at large scales small via fourth-order representation in the momentum equations, while retaining second order in temperature and moisture equations. The values of the diffusion parameters were tuned largely on the trade-off of lowering diffusion but keeping numerical stability in long runs. The lower diffusion also tends to increase the transient eddy variance which tends to improve surface stress climatology.