 |
|||||||||
|
|
|||||||||
|
|
|||||||||

Dynamical systems theory provides powerful tools to help understand
problems related to the complex climate system. The TCD group engages in the development of the theory, such as
bifurcation theory,
Boolean delay equations,
mixing and transport,
as well as their applications. Other theoretical efforts include
the stability of fluid flows
and
the dynamics of planetary orbits.
Delay equations for Boolean-valued variables (Boolean delay equations: BDEs) are an appropriate mathematical framework for such situations. The feedback thresholds results in the discrete, on-off character of the variables, and the interaction time scales of the feedbacks are expressed as delays. Systems of BDEs have been shown to exhibit complicated and fascinating types of behavior, similar to and also different from systems of ordinary or partial differential equations. The theory of BDEs, initiated about a decade ago, is still being actively developed.
The understanding of planetary orbits is based on Hamiltonian dynamics, averaging and perturbation theory. Due to their mutual gravitational attraction, planets perturb each other in various ways, on time scales of years and hundreds of years to thousands and millions of years. After averaging over the former, fast variations in their orbits, one obtains the so-called secular system. The dynamics of the linear part of this system can be described by its eigenmodes. One can make further simplifications by considering the phases of these modes relative to that of the largest one.
Numerical bifurcation theory
Many systems in nature exhibit different regimes of temporal evolution pattens, depending on the values of key parameters. Bifurcation theory, combined with recent developments in numerical techniques and computational resources, enables us to determine "when and how" the transition from one regime of behavior to another occurs. Examples can be found in the following TCD research projects' web pages:
low-frequency variability,
atmosphere-ocean interaction,
3-D ocean circulation, and
physical processes;
see also the
Department of Atmospheric Sciences brochure
(Theoretical
Climate Dynamics).
Boolean delay equations
The temporal evolution of many physical and biological systems is determined by feedback processes among the essential variables. The feedback mechanisms, in many cases, depend on a set of thresholds associated with the state variables; each feedback has a characteristic time scale.

The figure above shows the evolution of solutions, x1=x1(t) and x2=x2(t), for a system of two first-order BDEs that exhibits increase of complexity in time. As time progresses, the number of "jumps" per unit time increases according to a power law.
Mixing and transport
in systems with few degrees-of-freedom (d-o-f)
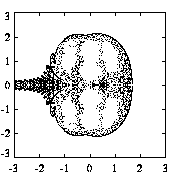 The applications of chaotic mixing and transport theory to the atmosphere and oceans are now being vastly expanded owing to two main reasons: 1) the development of the theory for systems with more than two d-o-f, and 2) improving computational resources and visualization techniques.
The applications of chaotic mixing and transport theory to the atmosphere and oceans are now being vastly expanded owing to two main reasons: 1) the development of the theory for systems with more than two d-o-f, and 2) improving computational resources and visualization techniques.
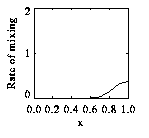
The figure at right shows a streak line around a pulsating dipole structure, called "thermon," in a two-layer model of oceanic flow, roughly indicating the mixing region. The figure at left shows the mixing rate between the dipoles interior and exterior regions as a function of the pulsation's amplitude.
Planetary orbits
The Earth's climate is influenced by external forcing such as variability in the Sun's radiative output and changes in the Earth's orbit and orientation in space. Solar irradiance varies on a wide range of time scales and it is far from completely understood. Orbital changes, however, are fairly well known for time spans of millions of years and they leave unmistakable signatures in records of past climates (see also Quaternary glaciation cycles). On time scales of tens of millions of years, however, the motion of planets is chaotic. While the effect of this chaos on the Earth's climate is difficult to ascertain, planetary orbits pose problems which are important and difficult in their own right.
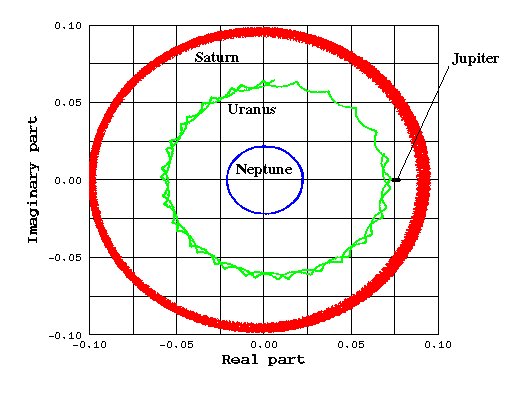
Our work on planetary motions includes topics such as Lie series, singularly weighted symplectic forms, the Great Inequality, secular resonances and the effects of dissipation on Hamiltonian dynamics. We also developed codes for the numerical integration of planetary orbits.
The latest results on Earth's orbital history show a particularly intriguing chaotic transition 65 million years ago which could be related to the KT impact.
TCD Members:
M. Ghil,
K. Ide, A. Saunders, F. Varadi
References:
Dee, D., and M. Ghil, l984: Boolean difference equations, I: Formulation and dynamic behavior, SIAM J. Appl. Math., 44, lll-l26.
Ghil, M., and A. Mullhaupt, l985: Boolean delay equations: periodic and aperiodic solutions, J. Stat. Phys., 41, l25-l74.
Ghil, M., and G. Wolansky, 1992: Non-Hamiltonian perturbations of
integrable systems and resonance trapping, SIAM J. Appl. Math.,
52, 1148-1171.
Ghil, M., F. Varadi, and W. M. Kaula, 1996: On the secular motion of the Jovian planets, Dynamics, Ephemerides and Astronomy in the Solar System, S. Ferraz-Mello, B. Morando and J. E. Arlot (Eds.), IAU Symp. No. 172, pp. 57-60.
Ide, K., and M. Ghil, 1995: An analytical study of geophysical flow estimation and mixing using extended Kalman filtering for vortex models. In Proc. 2nd WMO Ont'l Symp. on Assim. of Obs. in Meteor. & Oceanogr., Tokyo, March 1995, WMO/TD-No. 651, PWPR Report Series No. 5, WMO, Geneva, Switzerland, Vol. I, pp. 159-163.
Sakuma, H., and M. Ghil, 1990: Stability of stationary barotropic modons by Lyapunov's direct method, J. Fluid Mech., 211, 393-416.
Sakuma, H., and M. Ghil, 1991: Stability of propagating modons for small-amplitude perturbations, Phys. Fluids A, 3(3), 408-414.
Varadi, F., M. Ghil, and W. M. Kaula, 1995: The great inequality in a
Hamiltonian planetary theory, From Newton to Chaos, A. E. Roy and B. A. Stevens (Eds.), Plenum Press, NY, pp. 103-108.
Varadi, F., C. M. de la Barre, W. M. Kaula, and M. Ghil, 1995:
Singularly weighted symplectic forms and applications to asteroid motion, Celest. Mech. Dyn. Astron., 62, 23-41.
Wolansky, G., and M. Ghil, 1995: Stability of quasi-geostrophic flow
in a periodic channel, Phys. Lett. A, 202, 111-116.
Wolansky, G., and M. Ghil, 1996: An extension of Arnol'd's second
stability theorem for the Euler equations, Physica D, 94, 161-167.
Wolansky, G., M. Ghil and F. Varadi, 1996: Dynamical effects of the solar nebula's density gradient on asteroids in resonance with Jupiter,
Icarus, 132, 137-150.
Varadi, F., M. Ghil and W. M. Kaula, 1998: Jupiter, Saturn and the edge of chaos, Icarus, 139, 111-116.