Data assimilation is a methodology for estimating and forecasting the state of a fluid system -- the atmosphere or oceans -- from incomplete and inaccurate observations; the ultimate goal is to provide a dynamically consistent "motion picture" of the system with known error bars. Sequential estimation theory attempts to achieve this by combining the observations with the system's deterministic dynamical model repeatedly, as the observations become available.

Our interests in data assimilation include both the methodology and its applications to estimate and forecast the state of the system, help in improving models of its evolution, estimate key parameters of such models, and optimize observing-system design; the models range from highly idealized, such as coherent-vortex systems -- through intermediate, such as the Neelin-Jin model for the coupled tropical ocean-atmosphere system -- to complex models, such as the ocean general circulation model used for the Data Assimilation and Model Evaluation Experiments for the North Atlantic Basin (DAMEE-NAB).

Parameter estimation

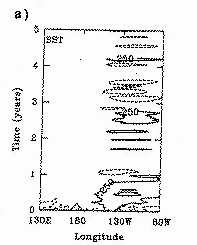
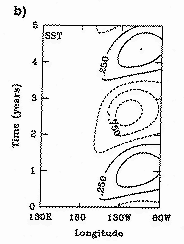
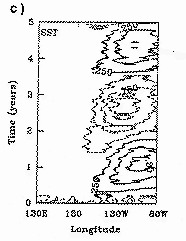
The figure shows a parameter estimation experiment for the tropical coupled atmosphere-ocean system. Time-longitude SST anomalies are plotted for a) a forecast using the model with incorrect coupling parameters, b) the corresponding reference solution with no wind-stress error, and c) assimilation results using the TOGA-TAO data to correct parameters. The contour interval is 0.5 degree (from Hao and Ghil, 1995).

Also see Department of Atmospheric Sciences brochure (Satellite-data assimilation).

TCD Members:
	M. Ghil, M. Chekroun, D. Kondrashov
References:
	Dee, D., S. E. Cohn, A. Dalcher, and M. Ghil, 1985: An efficient algorithm for estimating covariances in distributed systems, IEEE Trans. Automatic Control, AC-30, 1057-1065.
	Ghil, M., 1989: Meteorological data assimilation for oceanographers. Part I: Description and theoretical framework, Dyn. Atmos. Oceans, 13, 171-218.
	Ghil, M., 1997: Advances in sequential estimation for atmospheric and oceanic flows. J. Meteor. Soc. Japan, 75, 289-304.
	Ghil, M. and P. Malanotte-Rizzoli, 1991: Data assimilation in meteorology and oceanography, Adv. Geophys., 33, 141-266.
	Ghil, M. and R. Todling, 1996: Tracking atmospheric instabilities with the Kalman filter. Part II: Two-layer results, Mon. Wea. Rev., 124, 2340-2352.
	Ghil, M., M. Halem, and R. Atlas, l979: Time-continuous assimilation of remote-sounding data and its effect on weather forecasting, Mon. Wea. Rev., 107, l40-l7l.
	Ghil, M., S. Cohn, J. Tavantzis, K. Bube, and E. Isaacson, l98l: Applications of estimation theory to numerical weather prediction, Dynamic Meteorology: Data Assimilation Methods, L. Bengtsson, M. Ghil and E. Källén (Eds.), Springer Verlag, pp. l39-224.
	Ghil, M., K. Ide, and Numerical Prediction Division (Japan Meteorological Agency) (Eds.), 1995: Collection of Lecture Notes Presented at the Second WMO International Symposium on Assimilation of Observations in Meteorology and Oceanography, Special Issue, The Geophysical Magazine, Series 2, 1, Japan Meteorological Agency, Tokyo.
	Hao, Z., and M. Ghil, 1994: Data assimilation in a simple tropical ocean model with wind-stress errors, J. Phys. Oceanogr., 24, 2111-2128.
	Hao, Z., and M. Ghil, 1995: Sequential parameter estimation for a coupled ocean-atmosphere model. In Proc. 2nd WMO Int'l Symp. on Assim. of Obs. in Meteor. & Oceanogr., Tokyo, March 1995, WMO/TD-No. 651, PWPR Report Series No. 5, WMO Geneva, Switzerland, Vol. I, pp. 181-186.
	Ide, K., and M. Ghil, 1997a: Extended Kalman filtering for vortex systems. Part I: Methodology and point vortices. Dyn. Atmos. Oceans, 27, 301-332.
	Ide, K., and M. Ghil, 1997b: Extended Kalman filtering for vortex systems. Part II: Rankine vortices and observing-system design. Dyn. Atmos. Oceans, 27, 333-350.
	Ide, K., P. Courtier, M. Ghil, and A. Lorenc, 1997: Unified notation for data assimilation: Operational, sequential and variational. J. Meteor. Soc. Japan, 75, 181-189.
	International Programme Committee (D. L. T. Anderson, A. F. Bennett, P. Courtier, R. Daley, M. Ghil, Chair; K. Ide, Secretary; M. Kubota, K. Puri, P. Malanotte-Rizzoli, N. Sato, O. Talagrand, Eds.), 1995: Proceedings of the Second WMO International Symposium on Assimilation of Observations in Meteorology and Oceanography, Tokyo, March 1995, WMO/TD-No. 651, PWPR Report Series No. 5, World Meteorological Organization, Geneva, Switzerland, Vols. I & II, 717 pp.
	Jiang, S., and M. Ghil, 1993: Dynamical properties of error statistics in a shallow-water model, J. Phys. Oceanogr., 23, 2541-2566.
	Jiang, S., and M. Ghil, 1997: Tracking nonlinear solutions with altimetric data in a shallow-water model. J. Phys. Oceanogr., 27, 72-95.
	Miller, R. N., M. Ghil and F. Gauthiez, 1994: Advanced data assimilation in strongly nonlinear dynamical systems, J. Atmos. Sci., 51, 1037-1056.
	Panel on Model-Assimilated Data Sets (D. R. Johnson, J. R. Bates, G. P. Brasseur, M. Ghil, A. Hollingsworth, R. L. Jenne, K. Miyakoda, E. Rasmusson, E. S. Sarachik, and T. T. Warner), 1991: Four-Dimensional Model Assimilation of Data: A Strategy for the Earth System Sciences, National Academy Press, Washington, D.C., 78 pp.
	Todling, R., and M. Ghil, 1994: Tracking atmospheric instabilities with the Kalman filter. Part I: Methodology and one-layer results, Mon. Wea. Rev., 122, 183-204.