 |
 |
 |
 |
Once a data vector has been read in using the File/Data pull-down menu, selecting `B-T Correlogram' from the Analysis Tools menu launches the tool window. Figure 2a shows its state after pressing the Get Default Values button, see below:
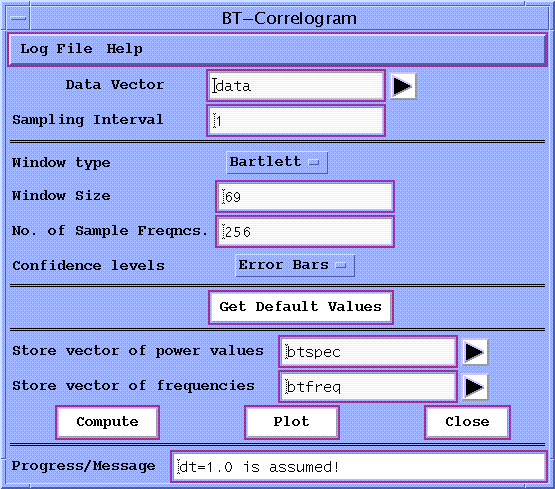
Figure 2a: B-T Correlogram window.
Here the user needs to specify the vector names of the data to be analyzed and computed results, the sampling interval, the window type and size, as well as the number of sample frequencies to be plotted. Default, as shown on Fig. 2, can be specified by pressing Get Default Values button. If the sampling interval is not specified, it is set to unity.
The Window type pull-down menu allows one to choose the shape of the windowing function to be applied in estimating the correlogram. The window shapes available are:
As Press et al. (1989) have noted, the choice of window functions is usually not as important as the choice of Window Size. The Get Default Values button allows a default choice of window size and the number of sample frequencies. The latter is actually forced by the Toolkit to be equal to a power of 2, and the power densities at this number of evenly-spaced frequencies between 0 and the Nyquist frequency 0.5/dt are estimated, where dt is the sampling interval of the data entered by the user in the Sampling Interval field. Thus, the units of the abscissa on all plots are cycles per sampling interval, over the range 0 to 0.5/dt.
The smaller the window size, the more independent samples are obtained for estimation purposes and therefore the smaller will be the variance of the spectral estimate. However, the smaller the window size, the lower the spectral resolution of the estimate will be. Note that the spectral resolution is independent of the number of sample frequencies. Robustness of results to changes in window type and length is the simplest test of their validity.
Two types of statistical Confidence Levels are provided, both of which apply a chi-squared test to calculate the 2.5% and 97.5% confidence levels. The Error Bars button computes the 95% uncertainty range about the spectral estimates themselves. The AR(1) button computes the 95% uncertainty range of a best-fit AR(1) red-noise process.
Running the tool using the Compute button at the bottom writes results to the specified internal vector names, which are given here by default. To save the results to a file, one would go to the File/Data pull-down menu on the main Spectra panel, and use the Write Vector function.
Finally, the resulting spectrum shown on Fig. 2b. is plotted using the Plot button .
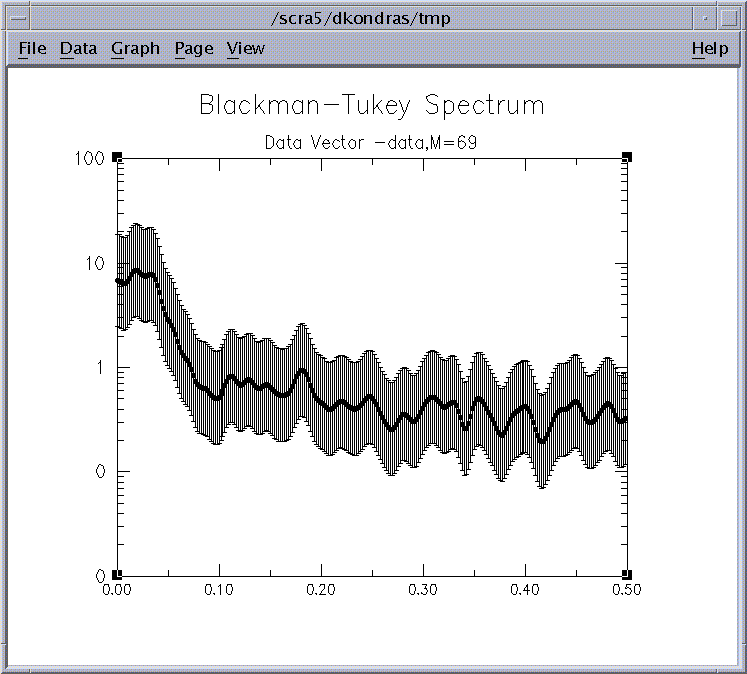
Figure 2b: B-T Correlogram.
 |
 |
 |
 |