3. TOOLKIT DEMONSTRATION

e. Singular-Spectrum Analysis

Selecting the `Singular Spectrum Analysis' button from the Analysis Tools menu on the main panel launches the following window (shows its state after pressing Get Default Values button, see below):

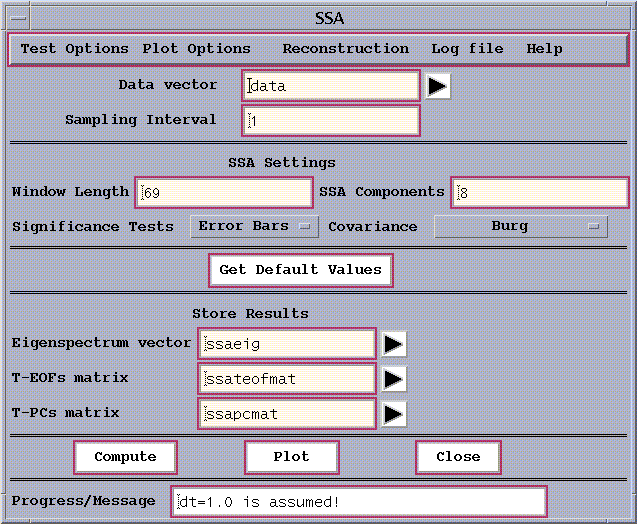
Figure 11: SSA control panel.

Having specified the data vector to be analyzed (here `data', the SOI time-series) and the sampling interval, the principal SSA options to be specified are the Window Length, the type of Significance Test, and Covariance Estimator. The number of SSA Components specifies how many components will be retained for future analyses. The Get Default Values button is provided as a guide.

Window Length

As a rule of thumb, the window length M should be chosen to be longer than number of data points in the oscillatory periods under investigation, and shorter than number of data points in the spells of an intermittent oscillation. Vautard et al. (1992) recommend that the window length be less than about N/5 where N is the number of points in the timeseries. Robustness of results to M is an important test of their validity. The choice of window length sets the dimension of the lag autocorrelation matrix to be constructed and diagonalized by SSA, and thus determines the computational burden of the application. Larger values of M correspond to higher spectral resolution, although there is no direct equivalence between them.

We will set the Window Length to 60, which is a good choice for out time series (690 data points with a one month sampling rate) and the oscillatory periods (2 and 4 years) under investigation.

Covariance Estimation

The method for estimating the autocovariance matrix that is decomposed (diagonalized) by SSA is chosen by selecting either `Burg' , `Vautard -Ghil' , or ` Broomhead &King ' from the `Covariance' button on the main SSA control panel (Fig. 11).

As indicated in the theoretical section, Burg estimation is an iterative process based on fitting an AR model with a number of AR components equal to the SSA window length. The Burg approach in principal should involve less "power leakage" due to the finite length of the time series and should therefore improve resolution (Penland et al., 1991). However, Vautard et al. (1992) found that the Burg estimate can induce significant biases when nonstationarities and very low-frequency variations are present in the series. Thus in some cases it will be worthwhile to try the Vautard et al. method. Also, for long series (N on the order of 5,000), the Vautard -Ghil estimate is less computationally burdensome and thus is completed more quickly.

In practice, we have found that the Vautard-Ghil method is more prone than is the Burg method to numerical instabilities (yielding negative eigenvalues) when pure oscillations are analyzed. Both the Burg and Vautard-Ghil methods impose a Toeplitz structure upon the autocovariance matrix whereas the Broomhead & King method does not. The Broomhead & King method is thus somewhat less prone to problems with nonstationary time series (Allen et al., 1992b), although the Vautard et al. method seems untroubled by all but the most extreme nonstationarities. The Toeplitz methods also impose symmetries on the EOF shapes whereas the Broomhead & King method does not. However the Toeplitz methods do appear to yield more stable results under the influence of minor perturbations of the time series (Allen and Smith,1996). 

NB: The Burg covariance matrix estimation option is not supported by MCSSA which defaults to Vautard-Ghil if Burg is selected on the main SSA panel.

We used Burg covariance method for analyzing SOI time series.

Significance tests

There are three choices for Significance test

described below. If Error Bars are selected, the eigenspectrum is displayed in order of eigenvalue rank. In the remaining two cases, the spectrum of eigenvalues is plotted against the dominant frequency associated with the respective T-EOF. Exception: the eigenspectrum-shape test in MCSSA is plotted against rank. 
The Test Options pull-down menu is used to set the preferences for the particular test, and is shown in Fig. 12. These options are explained in more details below.

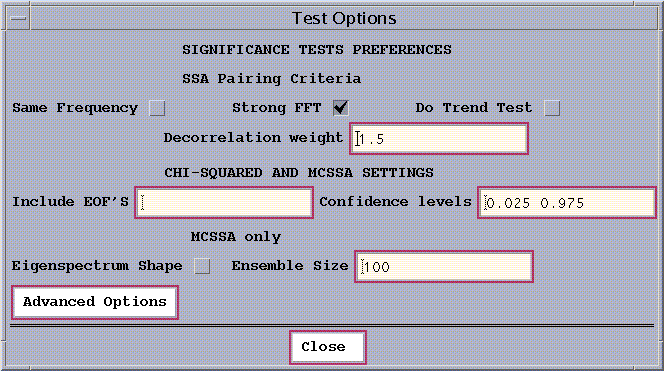
Figure 12: Test options control panel.

Error Bars Test

This is the default test. It constructs a set of ad-hoc error bars that are based on the estimated decorrelation time of the time series according to:

dli = (2kL/N)1/2 li

where L is a typical decorrelation time for the time series, k is a user supplied Decorrelation weight between 1 and 2 (1.5 by default), and li is the i-th eigenvalue in the spectrum. The Toolkit estimates L to be the inverse of the logarithm of the lag-one autocorrelation of the time series. Weights close to 1 are closer--but not generally equal to--the liberal error bars of Vautard and Ghil (1989); weights approaching 2 are closer to the conservative error bars of Ghil and Mo (1991a).

After we click the Compute and Plot buttons a graphics window will open to display the eigenvalue spectrum of the specified SSA. The units of abscissa are SSA component number (eigenvalue rank), and with the variance contributed by each SSA component on the ordinate.

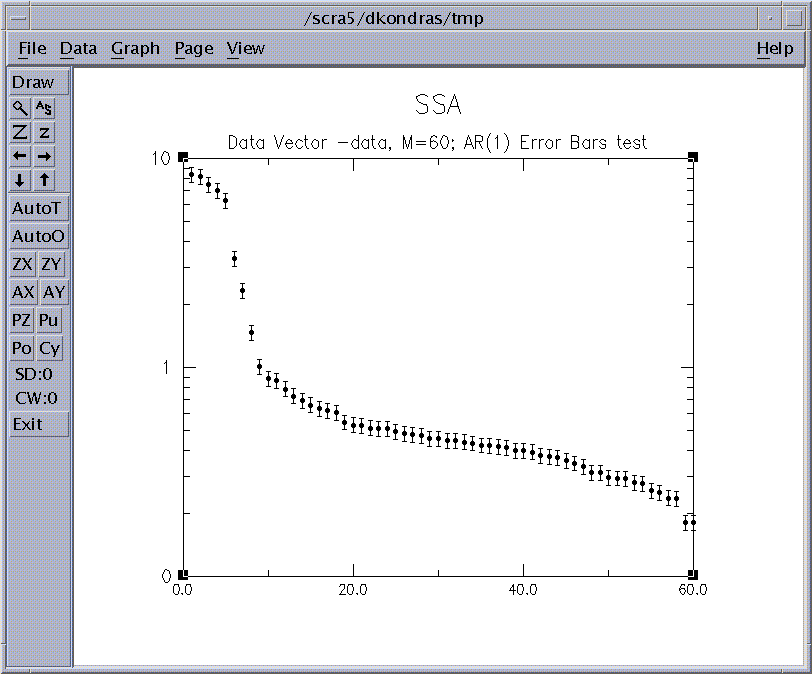
Figure 13: SSA eigenvalue spectrum for 'soi'.


Since the window length was set to 60, SSA decomposes the time series into 60 components and thus 60 eigenvalues are plotted. The significance of the various components can be judged qualitatively by noting which components contribute significantly more variance relative to the noise background. The latter in turn assumed to include the components that lie in the flattish tail of the eigenvalue spectrum, i.e. components from about 10 to 60. The leading 10 components in figure 11 lie above a distinct break in the eigenvalue spectrum, and thus may be of physical significance. In particular, we are interested in the leading four components which form two pairs of nearly equal eigenvalues. As discussed in the theory section above, pair of nearly equal eigenvalues in SSA is one of the characterising as oscillation. However, the eigenvalues are subject to numerical and sampling errors (North et al., 1982), and mere pairing of eigenvalues is not enough to guarantee that an oscillation has been identified. In the eigenvalue plot above, the error bars show an ad hoc range of the estimation errors. (See below for more sophisticated significance tests.) Any of the eigenvalues with significantly overlapping error bars could represent an "oscillatory pair'. Also eigenvalues with error bars that overlap significantly with the error bars of the noise part of the spectrum must also be suspected of being part of that noise.

Pairing Criteria

The Toolkit identifies potential oscillation components using 3 pairing criteria which can be activated concurrently using checkboxes in Fig. 12. (These 3 tests are performed on clusters of eigenvalues whose ad-hoc error bars overlap; however, it is not necessary for the 'Error Bars' test to be selected on the main SSA panel.) The results of these tests are written to the log file.

In the SOI example, the log file shows that component 1-2 meet both criteria for being oscillations. We will return to investigate the oscillations after considering some more of the controls in the SSA part of the menu.

Monte Carlo SSA and Chi-Squared test

The Monte Carlo SSA (MCSSA) significance test is described by Allen and Smith (1996). It tests significance against a red noise null-hypothesis. You may download test dataset of Allen and Smith (1996), if you want to reproduce the figures in that paper. A large ensemble of red-noise surrogate time series are generated, each with the same length and same expected lag-1 autocorrelation as the time series to be tested (but see note under 'Include EOFs' below).

Two fixed T-EOF bases are used, unless the eigenspectrum-shape test is invoked (see below).

`Include EOFs box': List of "signal" EOFs (by rank) to include in the noise null-hypothesis, from which the noise surrogates and null-hypothesis EOFs are computed. Note that irrespective of basis (data or null-hyp. EOFs), the characteristics of the noise, and thus the error bars are modified by including data EOFs. In fact the contribution of the latter to the lag-1 autocorrelation of the data time series are removed, when they are included in the null-hypothesis, see Allen and Smith (1996). If no data EOFs are specified, the null-hypothesis is pure AR(1) noise. Set of space-delimited integers. Not relevant to the 'Monte Carlo Eigenspectrum shape' test.

`Confidence levels box': Pair of confidence levels of the noise null-hypothesis to plot. For example, 0.05 and 0.95 would plot noise error bars spanning the 5th to 95th percentiles of the noise distribution. Two space-delimited reals.

`Ensemble Size': Number of Monte Carlo noise realizations.

Eigenspectrum Shape Monte Carlo test

`Eigenspectrum shape checkbox': This checkbox makes a fundamental change to the nature of the Monte Carlo test, making it a separate test. This test based on eigenspectrum shape, in which a new EOF basis is computed for each noise realization by diagonalizing its individual covariance matrix-- see Elsner and Tsonis (1994) or Dettinger et al. (1995). The ranked eigenvalue spectrum of the data is plotted along with chosen percentiles of the ranked eigenvalue spectra of the noise realizations.

Advanced Options: This button yields a control panel that allows the MCSSA "Data Basis", "Noise Basis" and the set of surrogates to be saved to a file, or read (NB: read function not yet implemented - sorry!) in from one. This may be useful if you want to use a custom-made basis, or you want to save a large ensemble of surrogates for future use. The red-noise coefficients used to generate the surrogates can also be overidden by inputting values here. Warning: If these files are not in the correct format, the Toolkit will crash!

Note on MCSSA temporary files: The MCSSA and Chi-squared tests generate a set of local files mcssac.* that are deleted upon exiting the Toolkit. If these files are needed, they must be copied/moved by hand using Unix. 

Chi-squared test

It follows the Monte Carlo SSA (MCSSA) approach (see above) in which red-noise surrogates are projected onto the basis consisting of the SSA eigenvectors (T-EOFs) of either the data or null-hypothesis covariance matrix. In contrast to MCSSA, the chi-squared test approximates the distribution of surrogate projections as chi-squared with 3M/N degrees of freedom. This is quite accurate for the case of sinusoidal EOFs and a linear (AR-type) noise null-hypothesis -- see Allen and Smith (1996), appendix. The probability of n excursions above the mth percentile is then estimated using the binomial distribution. This method is computationally fast compared to MCSSA which generates a large ensemble of surrogate noise series.
A typical testing procedure for Monte Carlo or Chi-Squared tests would be as follows (i) begin by testing against pure noise and identify frequencies at which the data displays anomalously high power against this null-hypothesis; (ii) find the data EOFs which correspond to these frequencies (being data-adaptive, these will often provide a better filter for the signal than the corresponding EOFs of the noise); finally (iii) re-test including these EOFs in the null-hypothesis to check if there are other features in the spectrum which were concealed by the dominant signal . It is, of course, consistent to iterate this procedure, but beware of the problem of test multiplicity discussed in Allen and Smith (1996) section 4.2: iteration makes the test increasingly liberal, so results which are still on the margins of acceptable significance after a couple of iterations including successively more EOFs into the "signal" should be ignored. 

Accordingly, to test against a pure red-noise null-hypothesis, we choose Chi-Squared as a significance test in the Test Options panel, leaving the Include EOFS field blank, as in Fig.12. After clicking the Compute and Plot buttons, the following graphics window will open:

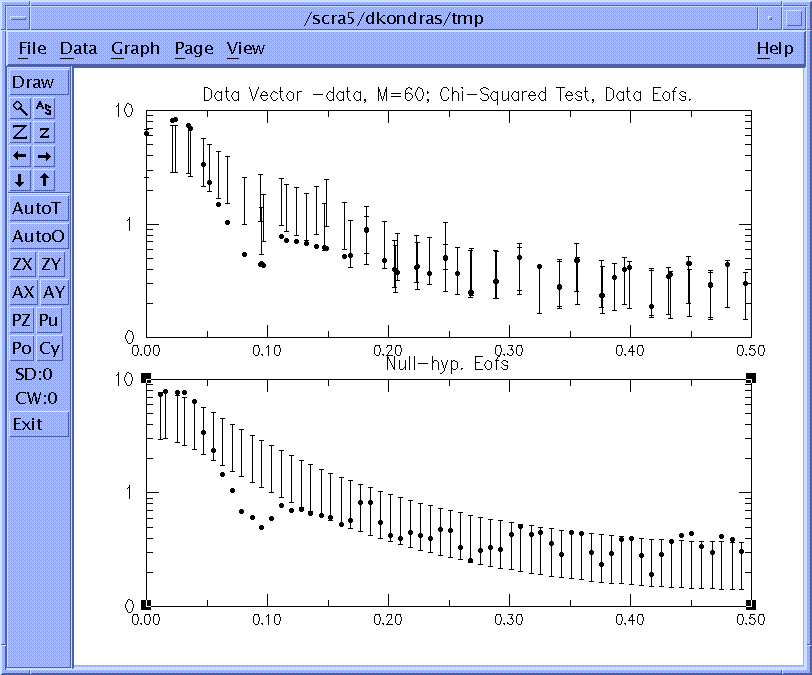
Figure 14: Chi-Squared test for 'soi'.


Both parts of Fig.14 have variance plotted against the dominant frequencies of 'basis' EOFs on x-axis, and describe projection of data and null-hypothesis (NH) surrogates onto 'basis' EOFs (see above). The dominant frequencies of EOFs are calculated with a 0.001/dt resolution in the Nyquist interval from 0 to 0.5/dt. The error bars represent 95% of variance (with settings of Confidence levels such as in Fig. 12) we expect to find in the state-space direction defined by a particular EOF from the 'basis', when analysing a segment of 'NH' noise. Using 'Include EOFS' option we can construct a composite 'NH' as described above, but it is a pure red-noise here. For the upper graph the 'basis' consists of the EOFs of the 'data' covariance matrix, and the projection of data gives us SSA eigenvalues plotted as dots.

For the lower graph, 'basis' EOFs are computed from the expected covariance matrix of the 'NH'. Projection of data does not give SSA eigenvalues here, but the interpretation of the graph is the same. Note how the EOFs of the pure noise NH are almost regularly spaced. According to Allen and Smith ('96) the NH basis avoids artificial varaiance-compression inherited in SSA and therefore it has a lower probability of false-positive results, i.e. identifying the noise components as significant.

For the Data Eofs basis we observe that eigenvalues corresponding to EOFS 1-2 and 3-4 appear almost superimposed on each other at frequencies equal to ~ 0.02 and 0.034 cycle/month, and lie outside the null-hypothesis error bars. Thus they are relatively unlikely ( at the 95% level, with settings of Confidence levels such as in Fig. 12.) to be merely due to selected null-hypothesis process, and represent two signficant oscilattions. The NH basis (lower graph) confirms the significance of these pairs, and we conclude that they correspond to the QB and QQ components of El Niño. The results of the Chi-squared test should always be checked using the Monte Carlo approach, which is also essential with more complex noise models.  We leave it as an exersise to the reader to check that similar results are obtained for our SOI time series with the Monte Carlo SSA test.

The T-EOFs, T-PCs and variances can be plotted using the Plot Options pull-down menu: 

Figure 15: SSA Plot Options.

The Reconstruction pull-down menu on the main SSA panel allows the reconstruction of the original timeseries from selected SSA components, specified as a space-delimited set of integers: 

Figure 16: SSA Reconstruction Window.


Selecting the identified 'significant' components 1-4, and After hitting the Compute and Plot buttons, a following graphics window will open:

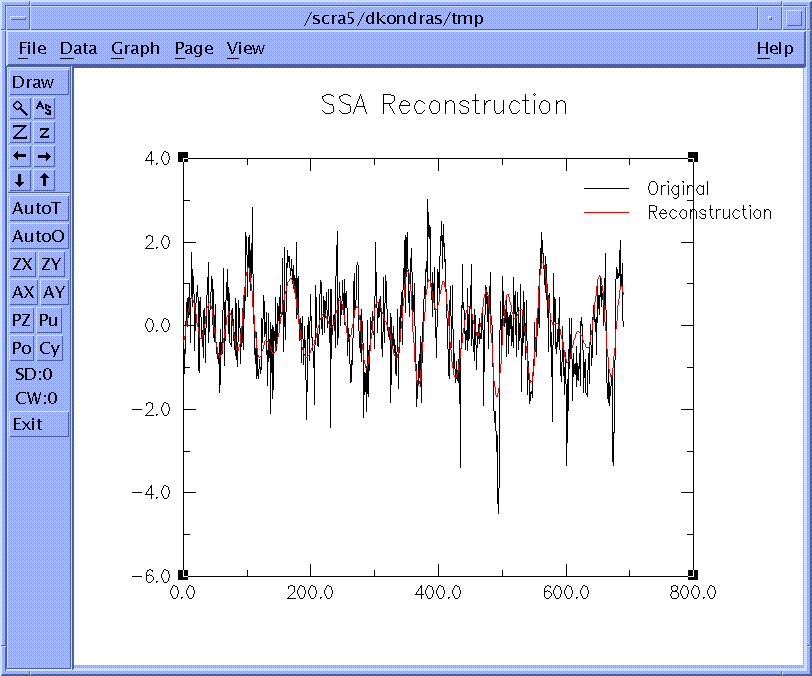
Figure 17: SSA Reconstruction.


Here the reconstructed signal is plotted against original timeseries, with a mean average removed. If this SSA-filtered RC series ('ssarcvec' vector) is now analyzed by MEM or MTM, the frequency spectrum of the RCs is much simpler than that of the complete time series, since most of the "noise" has been removed (Penland et al. 1991, Keppenne and Ghil 1992). The MEM Spectrum of SOI RCs series is plotted in Fig. 3c.
We leave as an excersise for the user to repeat SSA analysis with 11 SSA Components, and try to identify pair 10-11 with the oscillatory signal. Hint: this is related to the peak in MTM Spectrum at f~0.18 cycles/month.


Last modified: September 6, 2000