Over the last several years, we have developed a
three-dimensional numerical oceanic model intended for simulating currents,
ecosystems, biogeochemical cycles, and sediment movement in various coastal
regions. It is called the Regional Oceanic Modeling System (ROMS),
and it is closely related to the model developed at Rutgers University
with the same name.
Click on above
images for enlargement with caption.
ROMS Functionality and Southern
California Bight Projects
ROMS Scientists
Selected References
ROMS Functionality
- The model solves the hydrostatic
Primitive Equations in vertical hybrid z-sigma and horizontal
curvilinear coordinates with innovative algorithms for advection,
mixing, pressure gradient, vertical-mode coupling, time stepping, and
parallel efficiency (Shchepetkin and McWilliams, 1998, 2003,
2004). ROMS contains representations for the the following
additional elements:
- Surface fluxes of momentum, heat,
water, and materials with the atmosphere, including active coupling to
an atmospheric model.
- K-Profile Parameterization
(Large, McWilliams, and Doney, 1994) for top and bottom boundary
layers plus interior diapycnal mixing based on Richardson-number
threshold.
- Open-boundary conditions for
radiation, large-scale circulation, and tides (Marchesiello,
McWilliams, and Shchepetkin, 2001).
- 1-way and 2-way coupled,
sigma-level grid embedding for high-resolution subdomains (Penven et
al., 2006).
- Multi-decadal Pacific basin
simulations at coarse and eddy-permitting resolutions --> boundary
conditions for regional and local coastal domains.
- A single-group plankton ecosystem
(representing diatoms in an upwelling regime) plus OCMIP-style carbon
and oxygen cycles (Gruber et al., 2006a,b,c), or alternatively, a
recently implemented multi-group, multi-nutrient biogeochemical module
(Moore et al., 2002).
- Pollution dispersal and mixing
(Oram et al., 2006a,b).
- Lagrangian tracking, online and
offline, including behavioral movement (Capet and McWilliams, 2006).
- A data-assimilation and forecast
system, plus an adjoint model (with JPL; Li et al., 2006a,b).
- Particulate modeling: settling,
coagulation, sediment deposition, resuspension, transport, bed
structure, detrital remineralization (Blaas et al., 2006).
- Surface wave effects on currents
and tracers: combined wave-current bottom shear stress
parameterization, including prediction of ripples and enhanced
roughness related to waves and bed composition (Blaas et al., 2006)
plus Stokes vortex force, Bernoulli head, sea-level set-up, and Stokes
advection (McWilliams, Restrepo, and Lane, 2004) .
Southern California
Bight Ocean Modeling Projects at CESR, UCLA
last modified: June 18,
2010
APPROACH
The
regional oceanic responses in the Southern California Bight (SCB) to the
large-scale current system--including the California Current, the global
remote forcing through the coastal wave guide alongshore, the local and
remote forcing (atmospheric forcing, tides and waves), the local complexity
in the topography and coastline, and the intrinsic variabilities associated
with mesoscale to submesoscale transition--have been investigated with
comprehensive modeling frameworks. A key component in this pursuit this is
the Regional Oceanic Modelling System (ROMS, Schepetkin and McWilliams,
2005; 2008) that is a horizontal curvilinear and vertical terrain-following
coordinate, hydrostatic, incompressible, Boussinesq approximation,
free-surface oceanic circulation model with non-conservative forcing,
vertical and lateral diffusion, and bottom drag. It makes a
baroclinic-barotropic mode split, with explicit fast time-stepping and
subsequent conservative averaging of barotropic variables. Tremendous
effort has been made to expand the ROMS capabilities to include
non-hydrostatic dynamics (kanarska et al., 2007), surface gravity waves
(Uchiyama et al., 2010), and fundamental sediment transport dynamics (Blaas
et al., 2007). The large-scale influences are taken into account through a
nesting technique where multiple model domains are configured to
realistically determine significant oceanic signals on many different
scales. The actual nested model designs depends on what dynamics we would
like to detect, and thus varies from project to project. One example being
used for the Submesoscale Dynamics Project is as follows.
The
ROMS configuration consists of triple-nested model domains with an off-line,
one-way nesting technique that downscales from 5 km horizontal resolution
for the U. S. West Coast (L0), to 1 km resolution for the SCB (L1), to 250
m horizontal resolution for the Santa Monica and San Pedro Shelves (L2).
Each domain has 40 bottom topography-following levels vertically stretched
such that grid cell refinement occurs near the surface and the bottom. The
model topographies are given by the 30-second global SRTM30 bathymetry
(Becker et al., 2008: Marine Geodesy)
in general; whereas, the 3-second NOAA-NGDC coastal relief data set (http://www.ngdc.noaa.gov/mgg/coastal/crm.html)
is used for the near-shore regions depending on data availability. The
outermost L0 is forced by the monthly-averaged SODA version 2.0.4, a
POP-based assimilated global oceanic dataset (e.g. Carton et al., 1996: J. Geophys. Res.) as lateral
boundary conditions, a monthly-averaged QuikSCAT-ECMWF blended wind data (http://cersat.ifremer.fr/data/discovery/by_product_type/gridded_products/mwf_blended)
as a surface momentum stress, a monthly-average AVHRR pathfinder satellite
SST (http://podaac.jpl.nasa.gov/DATA_PRODUCT/SST/index.html)
and the COADS climatological dataset (http://www.ncdc.noaa.gov/oa/climate/coads/)
for the other surface fluxes. On L0, the monthly climatology of runoff from
major rivers (Dai and Trenberth, 2002: J.
Hydrometeorol.) is taken into account. The intermediate L1 and the
inner-most L2 are then driven by the corresponding parent ROMS model
solutions with daily (L0 to L1) and 2-hourly (L1 to L2) lateral boundary
update. All the surface boundary conditions for L1 and L2 are given by an
hourly atmospheric forcing by a double-nested WRF model (e.g., Michalakes
et al., 1998: In: Design of a
Next-Generation Regional Weather Research and Forecast Model: Towards
Teracomputing, World Scientific) on 18- and 6-km horizontal grid
spacings; the 6-km solution is used to force the ROMS L1 and L2 models with
a one-way coupling approach. Tides are included in L1 and L2 with TPXO 7.1
global tidal prediction (e.g., Egbert et al., 1994: J. Geophys. Res.) to force L1 at the lateral boundaries with
ten tidal major constituents (M2, S2, N2, K2, K1, O1, P1, Q1, Mf, and Mm)
that synthetically provide free-surface elevation and barotropic velocity
components at every barotropic time step by superposing on to the
daily-averaged boundary conditions from the L0 run. Intrinsic
three-dimensional tidal variabilities in L1 are then brought into the L2
run through the high-frequency, 2-hour boundary update. For more details on
the model configurations, one may wish to refer our journal articles, most
of which are indicated at the end of each project description.
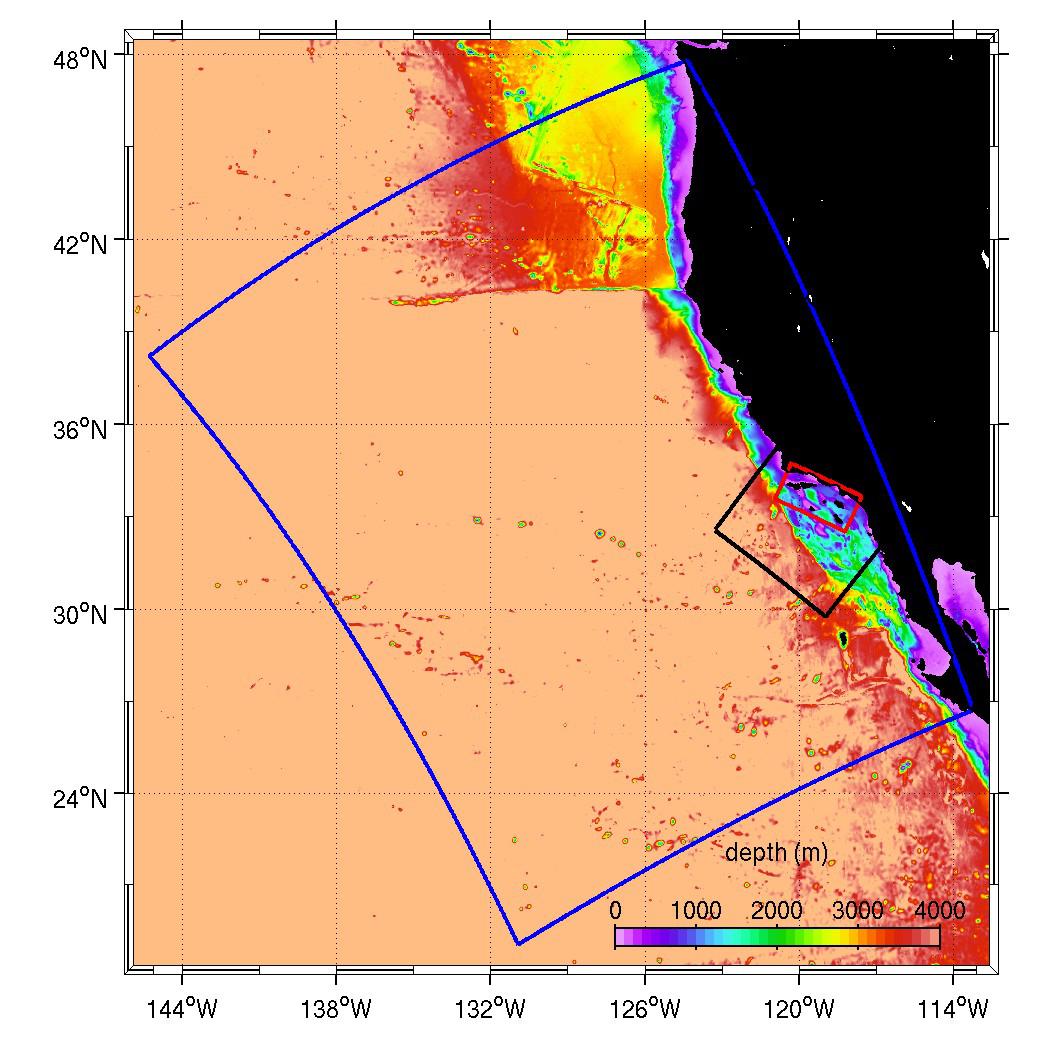
An example of
nested grid configurations used for the SCB projects. The figure shows
bathrmetry along the U.S. West Coast and perimeters of triple-nested ROMS
model domains (a descendant of the ICC configuration used for the
submesoscale dynamics project). The blue box is the outer most L0 domain
with a 5-km horizontal grid spacing, laterally forced by the SODA global
data. The black box is the intermediate L1 domain with a 1-km resolution
downscaled from ROMS L0, and the red box: the inner-most L2 domain with a
250-m resolution nested in ROMS L1.
Related
publication
·
A. F. Shchepetkin and J. C. McWilliams
(2005), The Regional Oceanic Modeling System: A split-explicit, free-surface,
topography-following-coordinate oceanic model, Ocean Modelling, 9,
347-404.
·
Y. Kanarska and A. F. Shchepetkin and J.
C. McWilliams (2007): Algorithm for non-hydrostatic dynamics in the
Regional Oceanic Modeling System, Ocean Modelling, 18, 143-174.
·
A. F. Shchepetkin and J. C. McWilliams
(2008): Computational kernel algorithms for fine-scale, multiprocess,
longtime oceanic simulations, In: Handbook of Numerical Analysis:
Computational Methods for the Ocean and the Atmosphere, Eds: R. Temam and
J. Tribbia, Elsevier Science, 119-182.
·
Y. Uchiyama, J. C. McWilliams and A. F.
Shchepetkin (2010): Wave–current interaction in an oceanic circulation
model with a vortex-force formalism: Application to the surf zone, Ocean Modelling, 34, 16-35,
doi:10.1016/j.ocemod.2010.04.002.
PROJECTS
1. Multi-Year,
Multi-Scale Oceanic Variabilities in the SCB
The
oceanic circulation in the Southern California Bight (SCB) is influenced by
the large-scale California Current offshore, tropical remote forcing
through the coastal wave guide alongshore, and local atmospheric forcing.
The region is characterized by local complexity in the topography and
coastline. All these factors engender variability in the circulation on
interannual, seasonal, and intraseasonal time scales. This study applies
the Regional Oceanic Modeling System (ROMS) to the SCB circulation and its
multiple-scale variability. The model is configured in three levels of
nested grids with the parent grid covering the whole U.S. West Coast. The
first child grid covers a large southern domain, and the third grid zooms
in on the SCB region. The three horizontal grid resolutions are 20 km, 6.7
km, and 1 km, respectively. The external forcings are momentum, heat, and
freshwater flux at the surface and adaptive nudging to gyre-scale SODA
reanalysis fields at the boundaries. The momentum flux is from a
three-hourly reanalysis mesoscale MM5 wind with a 6 km resolution for the
finest grid in the SCB. The oceanic model starts in an equilibrium state
from a multiple-year cyclical climatology run, and then it is integrated
from years 1996 through 2003. In this paper, the 8-year simulation at the 1
km resolution is analyzed and assessed against extensive observational
data: High-Frequency (HF) radar data, current meters, Acoustic Doppler
Current Profilers (ADCP) data, hydrographic measurements, tide gauges,
drifters, altimeters, and radiometers. The simulation shows that the
domain-scale surface circulation in the SCB is characterized by the
Southern California Cyclonic Gyre, comprised of the offshore equatorward
California Current System and the onshore poleward Southern California Countercurrent.
The simulation also exhibits three subdomainscale, persistent (i.e.,
standing), cyclonic eddies related to the local topography and wind
forcing: the Santa Barbara Channel Eddy, the Central-SCB Eddy, and the
Catalina-Clemente Eddy. Comparisons with observational data reveal that
ROMS reproduces a realistic mean state of the SCB oceanic circulation, as
well as its interannual (mainly as a local manifestation of an ENSO event),
seasonal, and intraseasonal (eddy-scale) variations. We find high correlations
of the wind curl with both the alongshore pressure gradient (APG) and the
eddy kinetic energy level in their variations on time scales of seasons and
longer. The geostrophic currents are much stronger than the wind-driven
Ekman flows at the surface. The model exhibits intrinsic eddy variability
with strong topographically related heterogeneity, westward-propagating
Rossby waves, and poleward-propagating coastally-trapped waves (albeit with
smaller amplitude than observed due to missing high-frequency variations in
the southern boundary conditions).
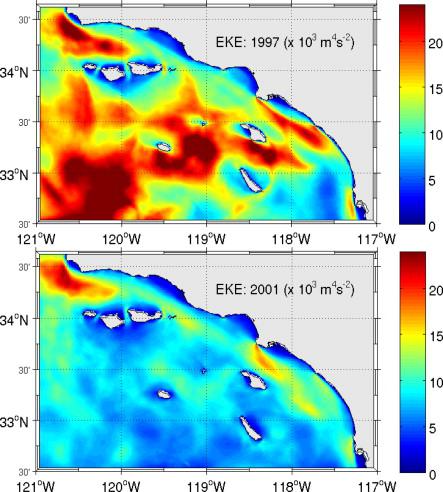
Maps
of the annual-mean surface EKE during the years with the largest and
smallest eddy energy: 1997 (top) and 2001 (bottom). The largest EKE occurs
during 1997 in association with the ENSO event, and the lowest EKE occurs
in 2001, with the 1997 level almost double that in 2001. The largest
changes in the EKE pattern are in the offshore central SCB and further
offshore in the California Current.
Related publication
·
Marchesiello, P., J.C.
McWilliams, and A. Shchepetkin (2003): Equilibrium structure and dynamics
of the California Current System. J.
Phys. Ocean. 33, 753-783.
·
C.
Dong, E. Y. Idica and J. C. McWilliams (2009): Circulation and
multiple-scale variability in the Southern California Bight, Progress in
Oceanography,82,168-190,doi:10.1016/j.pocean.2009.07.005.
2. Submesoscale Dynamics
in Eddying Flow Regimes
In
computational simulations of an idealized subtropical eastern boundary
upwelling current system, similar to the California Current, a submesoscale
transition occurs in the eddy variability as the horizontal grid scale is
reduced to O (1) km. The
transition in terms of the emergent flow structure and the associated
time-averaged eddy fluxes has been examined with ROMS. In addition to the
mesoscale eddies that arise from a primary instability in the alongshore,
wind-driven currents, significant energy is transferred into submesoscale
fronts and vortices in the upper ocean. The submesoscale arises through
surface frontogenesis growing off upwelled cold filaments that are pulled
offshore and strained in between the mesoscale eddy centers. In turn, some
submesoscale fronts become unstable and develop submesoscale meanders and
fragment into roll-up vortices. Associated with this phenomenon are a large
vertical vorticity and Rossby number; a large vertical velocity; a
relatively flat horizontal spectra (contrary to the prevailing view of
mesoscale dynamics); a large vertical buoyancy flux acting to restratify
the upper ocean; a submesoscale energy conversion from potential to
kinetic; a significant spatial and temporal intermittency in the upper
ocean; and a material exchanges between the surface boundary layer and
pycnocline. Comparison with available observations indicates that
submesoscale fronts and instabilities occur widely in the upper ocean, with
characteristics similar to the simulations.
The
emergent upper-ocean submesoscale fronts are analyzed from phenomenological
and dynamical perspectives, using a combination of composite averaging and
separation of distinctive subregions of the flow. The initiating dynamical
process for the transition is near-surface frontogenesis. The frontal
behavior is similar to both observed meteorological surface fronts and
solutions of the approximate dynamical model called surface dynamics (i.e.,
uniform interior potential vorticity q
and diagnostic force balance) in the intensification of surface density
gradients and in the secondary circulations as a response to a mesoscale
strain field. However, there are significant behavioral differences
compared to the surface-dynamics model. Wind stress acts on fronts through
nonlinear Ekman transport and creation and destruction of potential
vorticity. The strain-induced frontogenesis is disrupted by vigorous submesoscale
frontal instabilities that in turn lead to secondary frontogenesis events,
submesoscale vortices, and excitation of even smaller-scale flows.
Intermittent, submesoscale breakdown of geostrophic and gradient-wind force
balance occurs during the intense frontogenesis and frontal-instability
events.
The
mesoscale to submesoscale transition is mainly explained by the emergence
of ubiquitous submesoscale density fronts and ageostrophic circulations
about them in the weakly stratified surface boundary layer. Here the
high-resolution simulations are further analyzed from the perspective of
the kinetic energy (KE) spectrum shape and the spectral energy fluxes in
the mesoscale-to-submesoscale range in the upper ocean. For wavenumbers
greater than the mesoscale energy peak, there is a submesoscale power-law
regime in the spectrum with an exponent close to negative 2. In the KE balance an
important conversion from potential to kinetic energy takes place at all
wavenumbers in both mesoscale and submesoscale ranges; this conversion is
the energetic counterpart of the vertical restratification flux and
frontogenesis discussed in the earlier papers. A significant forward
cascade of KE occurs in the submesoscale range en route to dissipation at
even smaller scales. This is contrary to the inverse energy cascade of
geostrophic turbulence and it is, in fact, fundamentally associated with
the horizontally divergent (i.e., ageostrophic) velocity component. The
submesoscale dynamical processes of frontogenesis, frontal instability, and
breakdown of diagnostic force balance are all essential elements of the
energy cycle of potential energy conversion and forward KE cascade.
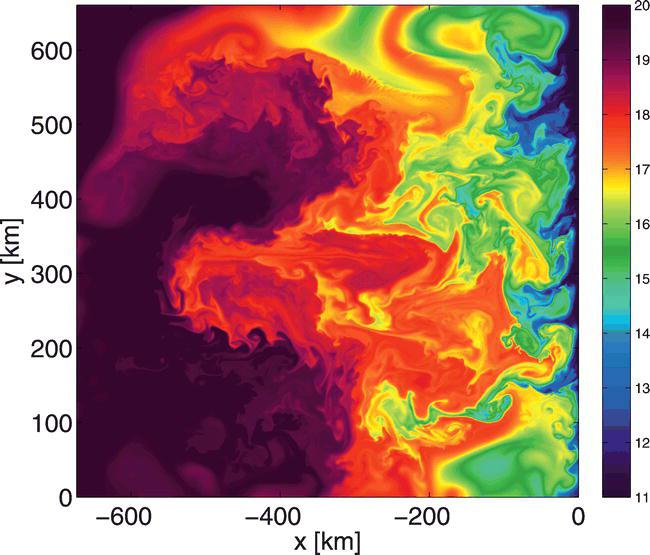
Instantaneous
surface temperature T (x, y) field at time t =
208 days after ICC initialization, as an example of a suite of
computational simulations for an idealized subtropical, eastern boundary,
upwelling current system [referred to as the idealized California Current
(ICC)]. Note the string of meanders and filaments in 17 to 19 degree
Centigrade water with wavelengths approximately 50 km running along the
edges of the offshore eddies. Notice also that an instability event is
located at (x equals
approximately negative 250 km, y
equals approximately 350 km); it separates waters in the range 16 to 18
degrees Centigrade, and the temperature front is roughly aligned with the x axis.
Related publication
·
X. Capet, J. C. McWilliams, M. J.
Molemaker, and A. F. Shchepetkin (2008a): Mesoscale to submesoscale
transition in the California Current System. Part I: Flow structure, eddy
flux, and observational tests. J.
Phys. Oceanogr., 38, 29–43.
·
X. Capet, J. C. McWilliams, M. J. Molemaker,
and A. Shchepetkin (2008b): Mesoscale to submesoscale transition in the
California Current System. Part II: Frontal processes. J. Phys. Oceanogr., 38,
44–64.
·
X. Capet, J. C. McWilliams, M. J.
Molemaker, A. F. Shchepetkin. (2008c): Mesoscale to Submesoscale Transition
in the California Current System. Part III: Energy Balance and Flux. Journal of Physical Oceanography 38, 2256-2269.
3. Wave-Driven Currents
and Their Effects on SCB Circulations
A
vortex-force formalism for the interaction of surface gravity waves and
currents is implemented in a three-dimensional (3D), terrain-following,
hydrostatic, oceanic circulation model [Regional Oceanic Modeling System:
ROMS; Schepetkin and McWilliams, 2005]. Eulerian wave-averaged current
equations for mass, momentum, and tracers are included in ROMS based on an
asymptotic theory by (McWilliams et al., 2004), plus non-conservative wave
effects due to wave breaking, associated surface roller waves, bottom
streaming, and wave-enhanced vertical mixing and bottom drag especially for
coastal and nearshore applications. The currents are coupled with a
spectrum-peak WKB wave-refraction model that includes the effect of
currents on waves, or, alternatively, a spectrum-resolving wave model
(e.g., SWAN) is used. The coupled system is applied to the nearshore surf
zone during the DUCK94 field measurement campaign. Model results are
compared to the observations, and the effects of the parameter choices are
investigated with emphasis on simulating and interpreting the vertical
profiles for alongshore and cross-shore currents. The model is further
compared to another ROMS-based 3D coupled model by (Warner et al., 2008)
with depth-dependent radiation stresses on a plane beach. In both tests the
present model manifests an onshore surface flow and compensating offshore
near-bed undertow near the shoreline and around the breaking point. In
contrast, the radiation-stress prescription yields significantly weaker
vertical shear. The currents' cross-shore and vertical structure is
significantly shaped by the wave effects of near-surface breaker
acceleration, vertical component of vortex force, and wave-enhanced
pressure force and bottom drag.
Conservative
wave effects on inner-shelf circulation are investigated in the Channel
Island region off Santa Barbara, California (referred to as SBC) using a
quadruple nested ROMS configuration bounded by the global SODA field,
downscaled from the Pacific basin at 12.5 km and to a half km grid
resolution for Southern California Bight. In addition to the synoptic
forcing and tides, idealized moderate waves ( uniform in space and time)
are imposed. Diagnosis is made for one spring-neap cycle in September 2006.
This is a case where radiation stress does not work well as for uniform
wave field leading to no radiation stress divergence. The SBC summer
thermocline is known to be shallow, around only 10-20 m, whereas waves
increase it by about 8 m, and overall the mixed-layer depth is deepened
about 15 % by wave-induced upper-current modification and associated
enhancement of vertical shear. A clockwise-rotating, anti-cyclone sits in
the middle of SBC, while prominent strengthening and modulation of such a
circulation occurs mainly due to Stokes-Coriolis effects in upper ocean
associated with waves. The upper-ocean averaged velocity magnitude and
angle are also modified by waves substantially: the magnitude is increased
by about 30 %, and the direction is rotated clockwise by about 6 degree.
The Stokes-Ekman layer is much deeper than the mixed layer depth and
reaches to about 60 m deep. Vortex force (VF) also plays a crucial role in
modifying the circulation through eddy modulation. The surface subtidal
eddy kinetic energy (EKE) has the maxima in the channel due to poleward
advection of submesoscale eddies, accentuated by waves by about 20 %,
partially attributed to change in mean advection of eddies associated with
Stokes-Coriolis force. In turn, a vortical Rossby number (relative vertical
vorticity over the background rotation), giving a ratio of mean vortex
force to mean Stokes-Coriolis force that suggests the VF contribution
reaches 60 % of the Stoke-Coriolis contribution where EKE is high.
Moreover, VF is predominant in the nearshore area that is a central arena
for eddy shedding: hence eddy-wave interaction by vortex force is crucial
in modulating eddies, which could lead to feedback to the main circulation
through Reynolds stress divergence.
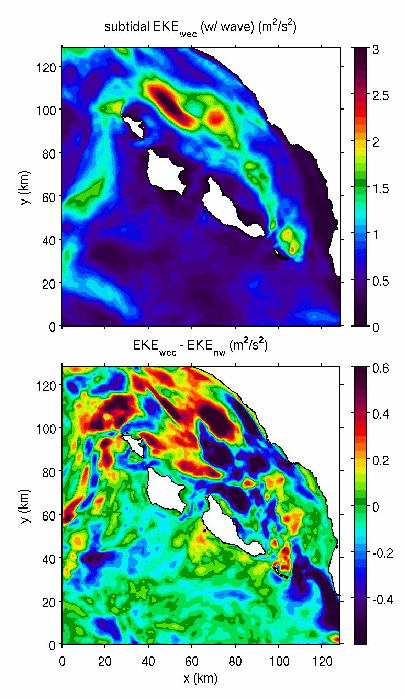
Wave
impact on upper-ocean turbulent kinetic energy (EKE) field in the SBC
(Santa Barbara Channel, CA). Upper panel: subtidal EKE in the SBC with wave
effects (EKEwec); lower panel: EKE difference, EKEwec
- EKEnw, where EKEnw is the one omitting wave
effects. The surface subtidal EKE (upper panel) has the maxima in the
channel due to poleward advection of submesoscale eddies, accentuated by
waves by about 20 % (lower panel), partially attributed to change in the
mean advection of eddies associated with Stokes-Coriolis force. In turn, a
vortical Rossby number (relative vertical vorticity over the background
rotation), gives a ratio of mean vortex force to mean Stokes-Coriolis
force, suggesting the VF contribution reaches 60 % of the Stoke-Coriolis
contribution where EKE is high.
Related publication
·
J. C. McWilliams, J. M. Restrepo and E.
M. Lane (2004): An asymptotic theory for the interaction of waves and
currents in coastal waters, Journal
of Fluid Mechanics, 511,
135-178, doi:10.1017/S0022112004009358.
·
Y. Uchiyama, J. C. McWilliams, and J. M.
Restrepo (2009), Wave-current interaction in nearshore shear instability
analyzed with a vortex force formalism, J.
Geophys. Res., 114, C06021, doi:10.1029/2008JC005135.
·
Y. Uchiyama, J. C. McWilliams and A. F.
Shchepetkin (2010): Wave–current interaction in an oceanic circulation
model with a vortex-force formalism: Application to the surf zone, Ocean Modelling, 34, 16-35,
doi:10.1016/j.ocemod.2010.04.002.
4. Generation and
Propagation of Internal Tides in SCB
To
be added...
5. Island-Induced Wakes
and Their Impact on Circulation
With
the existence of eight substantial islands in the Southern California
Bight, the oceanic circulation is significantly affected by island wakes.
In this paper a high-resolution numerical model (on a 1km grid), forced by
a high-resolution wind (2 km), is used to study the wakes. Island wakes
arise due both to currents moving past islands and to wind wakes that force
lee currents in response. A comparison between simulations with and without
islands shows the surface enstrophy (i.e., area-integrated square of the
vertical component of vorticity at the surface) decreases substantially
when the islands in the oceanic model are removed, and the enstrophy
decrease mainly takes place in the areas around the islands. Three cases of
wake formation and evolution are analyzed for the Channel Islands, San
Nicolas Island, and Santa Catalina Island. When flows squeeze through gaps
between the Channel Islands, current shears arise, and the bottom drag
makes a significant contribution to the vorticity generation. Downstream
the vorticity rolls up into submesoscale eddies. When the California
Current passes San Nicolas Island from the northwest, a relatively strong
flow forms over the shelf break on the northeastern coast and gives rise to
a locally large bottom stress that generates anticyclonic vorticity, while
on the southwestern side, with an adverse flow pushing the main wake
current away from the island, positive vorticity has been generated and a
cyclonic eddy detaches into the wake. When the northward Southern
California Countercurrent passes the irregular shape of Santa Catalina
Island, cyclonic eddies form on the southeastern coast of the island, due
primarily to lateral stress rather than bottom stress; they remain coherent
as they detach and propagate downstream, and thus they are plausible
candidates for the submesoscale spirals on the sea seen in many satellite
images. Finally, the oceanic response to wind wakes is analyzed in a
spin-up experiment with a time-invariant wind that exhibits strips of both
positive and negative curl in the island lee. Corresponding vorticity
strips in the ocean develop through the mechanism of Ekman pumping.
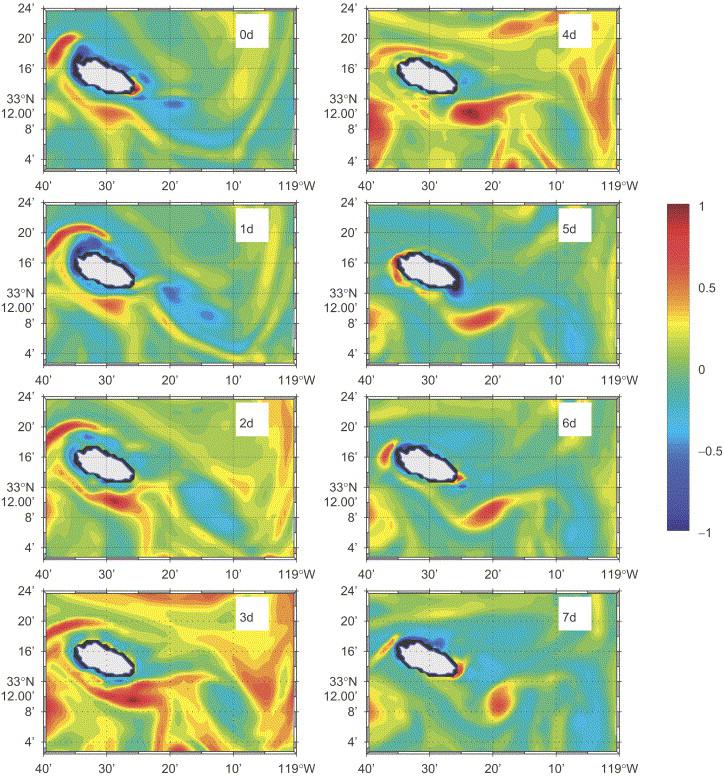
San Nicolas Island wake:
sequence of normalized surface vorticity (zeta) maps from March 21 to 28,
2002. March 21 = day 0. When current passes San Nicolas Island from the
northwest, an island wake forms. A time series of 8 days for the surface
vorticity is plotted, showing the formation and detachment of a cyclonic
eddy and the decaying progression of an anticyclonic eddy in the wake.
While the cyclonic eddy remains coherent, the anticyclonic eddy becomes
weaker and weaker as it is advected downstream. Asymmetry in the robustness
of cyclonic and anticyclonic wake eddies can be due to the weakening effect
of centrifugal instability on the latter when zeta is smaller than -f, as
occasionally occurs in the figure.
Related publication
·
C. Dong
and J. C. McWilliams (2007): A
numerical study of island wakes in Southern California Bight, Continental Shelf Research, 27,
1233-1248.
·
C. Dong, J. C. McWilliams and A. F. Shchepetkin
(2007): Island wakes in deep water, Journal
of Physical Oceanography, 37,
962-981.
6. Sediments and
material dispersal in SCB
Suspended
sediment-transport processes in Santa Monica and San Pedro Bay are analyzed
using the sediment-transport capabilities of the Regional Oceanic Modeling
System (ROMS). A one-month simulation for December 2001 has been carried
out with a set of nested domains. The model inputs include tides, winds,
surface waves, and idealized initial sediment conditions for sand and
non-cohesive silt. Apart from the control run, the sensitivity of the
results to surface waves, ripple roughness and bed armoring has been
analyzed. From the control experiment, the horizontal transport of sand
turns out to be limited to within a few km of the nearshore erosion zones.
During high wave events, silt is transported over further distances and
also partly offshelf in distinct plumes. The effectiveness of horizontal
silt transport depends strongly on vertical mixing due to both surface wind
stress and wave-enhanced bottom stress. High wave events coincident with
strong winds (hence strong vertical mixing) are the most optimal conditions
for sediment-transport. Excluding wave effects in the simulation shows that
surface waves are the dominant factor in resuspending bed material on the
Southern Californian shelves. The sensitivity experiments also show that
the direct influence of additional ripple roughness on erosion and
deposition is relatively weak. Switching off bed armoring locally results
in increases of near-bottom concentrations by a factor of 20 for silt and a
factor of 5 for sand as well as stronger spatial gradients in grain size.
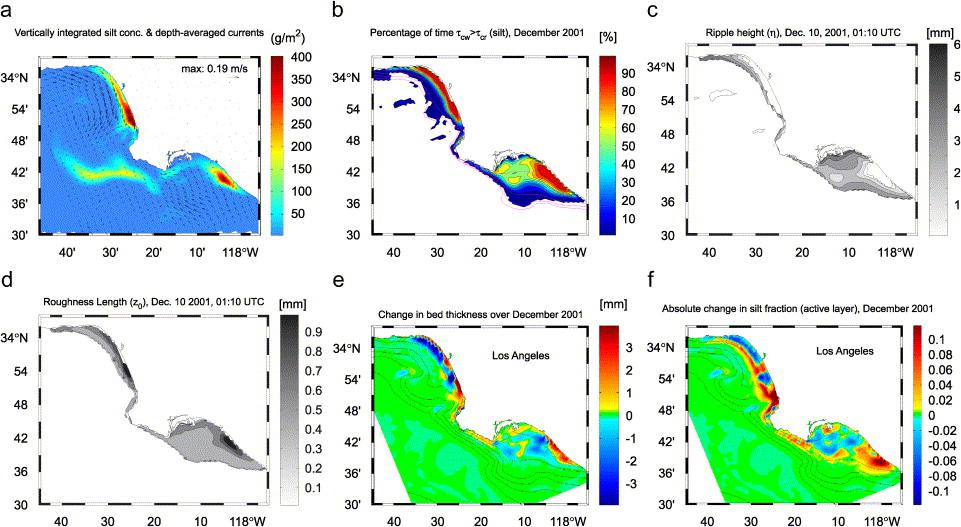
(a)
Depth-averaged, tide-averaged velocity and vertically integrated silt
concentration, half a day after maximum of December 15 wave event.
Concentrations locally up to 500 g/m2>. (b) Fraction of time
that wavecurrent bottom stress exceeds the threshold for silt suspension,
i.e.,T cw>Tcr,silt
. Dotted lines: 20 to 65 m isobaths (15 m interval). (c) Ripple height
(h) at the peak of 10 December wave event. (d) Bed roughness (including
ripple roughness and bed-load roughness) at the peak of 10 December wave
event. (e) Net change in bed thickness over December 2001 control experiment.
Red: net deposition; blue: net erosion. Color range -4 to 4 mm, data range
-28 to 11 mm (extremes just off Redondo Beach). Also shown are 15, 30, 60,
120, 240, 480 m isobaths. (f) As (e) but for net change in silt fraction of
the active layer. Color range -0.12 to 0.12, data range -0.12 to 0.39
(extremes in nearshore areas).
Related publication
·
M. Blaas, C. Dong, P. Marchesiello, J.C.
McWilliams, K.D. Stolzenbach (2007): Sediment-transport modeling on
Southern Californian shelves: A ROMS case study. Continental
Shelf Research , 27, 832-853.
PEOPLE
ROMS Scientists
The roster of scientists at UCLA currently working with ROMS is
Charles Dong,
Hartmut Frenzel,
Jim McWilliams,
Francois Colas,
Yusuke Uchiyama,
Jaison Kurian,
Jeroen Molemaker,
Florian Lemarie,
Claire Menesguen,
Peng Wang,
Alexander Shchepetkin,
Keith
Stolzenbach.
In addition, there are active collaborations with scientists at AGRIF, JPL, Marchesiello at IRD,
Rutgers,and Hall UCLA WRF.

UCLA ROMS group photo in
2010.
Back: Jaison Kurian, Jun Hong Liang, Jim McWilliams, Maarten Buijsman,
Yusuke Uchiyama, Alexander Shchepetkin, Jeroen Molemaker.
Front: Ed Huckle, Florian Lemarie, Guillaume Roullet, Francois Colas,
Claire Menesguen, and Peng Wang.
Selected References
Blaas, M., C. Dong, P. Marchesiello, J.C. McWilliams, and K.D. Stolzenbach,
2007: Sediment transport modeling on Southern Californian shelves: A ROMS
case study. Contin. Shelf Res. 27, 832-853.
Buijsman, M.C., Y. Kanarska, and J.C. McWilliams, 2010: On the generation
and evolution of nonlinear internal waves in the South China Sea. J.
Geophys. Res., 115, C02012, doi:10.1029/2009JC005275.
Buijsman, M.C., J.C. McWilliams, and C.R. Jackson, 2010: East-west
asymmetry in nonlinear internal waves from Luzon Strait. J. Geophys. Res.,
in press.
Blanke, R., C. Roy, P. Penven, S. Speich, J.C. McWilliams, and G. Nelson,
2002: Linking wind and interannual upwelling variability in a regional
model of the southern Benguela. Geophys. Res. Lett. 29,
41(1)-41(4).
Caldeira, R.M.A., P. Marchesiello, N. Nezlin, P. DiGiacomo, and J.C.
McWilliams, 2005: Island wakes in the Southern California Bight. J.
Geophys. Res., 110, C11012 - 1-20 (text) plus 6 pages of color figures.
Capet, X.J., P. Marchesiello, and J.C. McWilliams, 2004: Upwelling response
to coastal wind profiles. Geophys. Res. Lett. 31 (13),
L13311/1--L13311/4.
Capet, X., J.C. McWilliams, M.J. Molemaker, and A. Shchepetkin, 2008:
Mesoscale to submesoscale transition in the California Current System. I:
Flow structure, eddy flux, and observational tests. J. Phys. Ocean,, 38,
29-43.
Capet, X., J.C. McWilliams, M.J. Molemaker, and A. Shchepetkin, 2008:
Mesoscale to submesoscale transition in the California Current System. II:
Frontal processes. J. Phys. Ocean., 38, 44-64.
Capet, X., J.C. McWilliams, M.J. Molemaker, and A. Shchepetkin, 2008:
Mesoscale to submesoscale transition in the California Current System. III:
Energy balance and flux. J. Phys. Ocean. 38, 2256-2269.
Carr, S.D., X.J. Capet, J.C. McWilliams, J.T. Pennington, and F.P. Chavez,
2008: The influence of diel vertical migration on zooplankton transport and
recruitment in an upwelling region: Estimates from a coupled
behavioral-physical model. Fisheries Ocean., 17, 1-15.
Chao, Y., Z. Li, J. Farrara, J.C. McWilliams, J. Bellingham, X. Capet, F.
Chavez, J.-K. Choi, R. Davis, J. Doyle, D.M. Frantaoni, P. Li, P.
Marchesiello, M.A. Moline, J. Paduan, and S. Ramp, 2009: Development,
implementation, and evaluation of a data-assimilative ocean forecasting
system off the central California coast. Deep-Sea Res. II, 56, 100-126.
doi:10.1016/j.dsr2.2008.08.011.
Colas, F., X. Capet, J.C. McWilliams, and A. Shchepetkin, 2008: 1997-98 El
Nino off Peru: A numerical study. Prog. Ocean., 79, 138-155.
Di Lorenzo, E., A.J. Miller, N. Schneider, and J.C. McWilliams, 2005: The
warming of the California Current: Dynamics, thermodynamics and ecosystem
implications. J. Phys. Ocean., 35, 336-362.
Di Lorenzo, E.D., N. Schneider, K.M. Cobb, P.J.S. Franks, K. Chhak, A.J.
Miller, J.C. McWilliams, S.J. Bograd, H. Arango, E. Curchitser, T.M.
Powell, and P. Pieiere, 2008: North Pacific Gyre Oscillation links ocean
climate and ecosystem change. Geophys. Res. Lett., 35 L08607,
doi:10.1029/2007GL032838.
Dong, C., J.C. McWilliams, and A.F. Shchepetkin, 2007: Island wakes in deep
water. J. Phys. Ocean., 37, 962-981.
Dong, C., and J.C. McWilliams, 2007: A numerical study of island wakes in
the Southern California Bight. Cont. Shelf Res., 27, 1233-1248.
Dong, C., E.Y. Idica, and J.C. McWilliams, 2009: Circulation and
multiple-scale variability in the Southern California Bight. Prog.
Oceanography, 82, 168-190.
Dong, C., T. Mavor, F. Nencioli, S. Jiang, Y. Uchiyama, J.C. McWilliams, T.
Dickey, M. Ondrusek, H. Zhang, and D.K. Clark, 2009: An oceanic cyclonic
eddy on the lee side of Lanai Island, Hawai'i. J. Geophys. Res. 114,
C12001. doi:10.1029/2008JC005258.
Fringer, O., J.C. McWilliams, R.L. Street, 2006: A new hybrid model for
coastal simulations. Oceanography 19, 46-59.
Gruber, N., H. Frenzel, S.C. Doney, P. Marchesiello, J.C. McWilliams, J.R.
Moisan, J. Oram, G.K. Plattner, and K.D. Stolzenbach, 2006: Eddy-resolving
simulations of plankton ecosystem dynamics in the California Current
System: Part I: Model description, evaluation, and ecosystem structure.
Deep Sea Res. I, 53, 1483-1516.
Jin, X., C. Dong, J. Kurian, J.C. McWilliams, D.B. Chelton, and Z. Li,
2009: SST-Wind interaction in coastal upwelling: Oceanic simulation with
empirical coupling. J. Phys. Ocean., 39, 2957-2970.
Kanarska, Y., A. Shchepetkin, and J.C. McWilliams, 2007: Algorithm for
non-hydrostatic dynamics in the Regional Oceanic Modeling System. Ocean
Modelling, 18, 143-174.
Liang, J.H., J.C. McWilliams, and N. Gruber, 2009: The high-frequency
response of the ocean to mountain gap winds in the northeastern tropical
Pacific. J. Geophys. Res., 114, C12005. doi:10.1029/2009JC005370.
Li, Z., Y. Chao, and J.C. McWilliams, 2006: Computation of the
streamfunction and velocity potential for limited and irregular domains.
Mon. Weather Rev., 134, 3384-3394.
Li, Z., Y. Chao, J.C. McWilliams, and K. Ide, 2008: A three-dimensional
variational data assimilation system for the Regional Ocean Modeling
System: Implementation and basic experiments. J. Geophys. Res., 113,
C05002. doi:10.1029/2006JC004042.
Li, Z., Y. Chao, J.C. McWilliams, and K. Ide, 2008: A three-dimensional
variational data assimilation system for the Regional Ocean Modeling
System. J. Atmos. Ocean. Tech. 25, 2074-2090.
Marchesiello, P., J.C. McWilliams, and A. Shchepetkin, 2001: Open boundary
conditions for long-term integration of regional ocean models. Ocean
Modelling 3, 1-20.
Marchesiello, P., J.C. McWilliams, and A. Shchepetkin, 2003: Equilibrium
structure and dynamics of the California Current System. J. Phys. Ocean.
33, 753-783.
Mason, E., M.J. Molemaker, A. F. Shchepetkin, F. Colas, J.C. McWilliams,
and P. Sangra, 2010: Procedures for offline grid nesting in regional ocean
models. Ocean Modelling, 35, 1-15.
McWilliams, J.C., J.M. Restrepo, and E.M. Lane, 2004: An asymptotic theory
for the interaction of waves and currents in coastal waters. J. Fluid
Mech. 511, 135-178.
McWilliams, J.C., 2007: Irreducible imprecision in atmospheric and oceanic
simluations. Proc. Nat. Acad. Sci. 104, 8709-8713.
McWilliams, J.C., 2009: Targeted coastal circulation phenomena in
diagnostic analyses and forecasts. Dyn. Atmos. Oceans, 48, 3-15.
doi:10.1016/j.dynatmoce.2008.12.004
Mitarai, S., D.A. Siegel, J.R. Watson, C. Dong, and J.C. McWilliams, 2009:
Quantifying connectivity in the coastal ocean with application to the
Southern California Bight. J. Geophys. Res., 114, C10026.
doi:10.1029/2008JC005166
Moore, J.K., S.C. Doney, J.A. Kleypas, D.M. Glover, I. Y. Fung, 2002: An
intermediate complexity marine ecosystem model for the global domain.
Deep-Sea Res. II 49, 403-462.
Nagai, T., A. Tandon, N. Gruber, and J.C. McWilliams, 2008: Biological and
physical impacts of ageostrophic frontal circulations driven by confluent
flow and vertical mixing. Dyn. Atmos. and Oceans, 45, 229-251.
doi:10.1016/j.dynatmoce.2007.12.001.
Nencioli, F., C. Dong, T. Dickey, L. Washburn, and J.C. McWilliams, 2010: A
vector geometry based eddy detection algorithm and its application to a
high-resolution numerical model product and high-frequency radar surface
velocities in the Southern California Bight, J. Tech. Ocean., 27, 564-579.
doi:10.1175/2009JTECHO725.1
Nezlin, N., and J.C. McWilliams, 2003: Satellite data empirical orthogonal
functions statistics and the 19971998 El Nino off California. Remote
Sensing Envir. 84, 234-254.
Oram, J.J., J.C. McWilliams, \& K.D. Stolzenbach, 2008: Gradient-based
edge detection and feature classification of sea-surface images of the
Southern California Bight. {\it Remote Sensing of Environment} {\bf 112},
2397-2415. >br>
Penven P., L. Debreu, P. Marchesiello, and J.C. McWilliams, 2006:
Evaluation and application of the ROMS 1-way embedding procedure to the
California Current Upwelling System. Ocean Modelling, 12, 157-187.
Plattner, G. K-., N. Gruber, H. Frenzel, and J.C. McWilliams, 2005:
Decoupling marine export production from new production. Geophys.
Res. Lett. 32, L11612/1-4.
Sangra, P., A. Pascual, A. Rodriguez-Santana, F. Machin, E. Mason, J.C.
McWilliams, J.-L. Pelegri, C. Dong, A. Rubio, J. Aristegui, A.
Marrero-Diaz, A. Hernandez-Guerrez, A. Hernandez-Guerra, A.
Mertinez-Marrero, and M. Auladell, 2009: The Canary Eddies Corridor: A
major pathway for long-lived eddies in the subtropical North Atlantic. Deep
Sea Res. I, 56, 2100-2114.
Shchepetkin, A.F.,and J.C. McWilliams, 2009: Correction and Commentary for
``Ocean Forecasting in Terrain-Following Coordinates: Formulation and Skill
Assessment of the Regional Ocean Modeling System'' by Haidvogel et al., J.
Comp. Phys. 227, pp. 3595-3624. J. Comp. Phys., 228, 8985-9000.
Shchepetkin, A., and J.C. McWilliams, 1998: Quasi-monotone advection
schemes based on explicit locally adaptive dissipation. Monthly
Weather Rev. 126, 1541-1580.
Shchepetkin, A.F., and J.C. McWilliams, 2003: A method for computing
horizontal pressure-gradient force in an ocean model with a non-aligned
vertical coordinate. J. Geophys. Res. 108, 35.1-35.34.
Shchepetkin, A.F., and J.C. McWilliams, 2005: The Regional Oceanic Modeling
System: A split-explicit, free-surface, topography-following-coordinate
ocean model. Ocean Modelling 9, 347-404.
Shchepetkin, A.F., and J.C. McWilliams, 2008: Computational kernel
algorithms for fine-scale, multiprocess, longtime oceanic simulations. In:
Handbook of Numerical Analysis: Computational Methods for the Ocean and the
Atmosphere, R. Temam and J. Tribbia, eds., Elsevier Science, 119-181.
Uchiyama, Y., J.C. McWilliams, and A.F. Shchepetkin, 2010: Wave-current
interaction in an oceanic circulation model with a vortex-force formalism:
Application to the surf zone. Ocean Modelling, in press.
Xin, J., N. Gruber, H. Frenzel, S.C. Doney, and J.C. McWilliams, 2008: The
impact on atmospheric CO_2 of iron fertilization induced by the ocean's
biological pump. Biogeosciences, 5, 385-406.
Wang, X., Y. Chao, C. Dong, J. Farrara, Z. Li, J.C. McWilliams, J.D. Paduan,
and L.K. Rosenfeld,, 2009: Modeling tides in Monterey Bay, California.
Deep-Sea Res. II, 56, 219-231. doi:10.1016/j.dsr2.2008.08.012.
Watson, J.R., S. Mitarai, D.A. Siegel, J. Caselle, C. Dong, and J.C.
McWilliams, 2010: Realized and potential larval connectivity in the
Southern California Bight. Marine Ecology Prog. Series, 401, 31-48. doi:
10.3354/meps08376w
|