 |
 |
 |
 |
The Multi-Taper method (MTM) of spectral analysis provides a novel means for spectral estimation (Thomson, 1982; Percival and Walden, 1993) and signal reconstruction (e.g., Park, 1992) of a time series which is believed to exhibit a spectrum containing both continuous and singular components. This method has been widely applied to problems in geophysical signal analysis, including analyses of atmospheric and oceanic data (Ghil and Vautard, 1991; Kuo et al, 1990; Mann and Park, 1993;1994;1996b; Lall and Mann, 1995; Mann et al, 1995a; Thomson 1995; Mann and Park, 1996a) paleoclimate data (Berger et al, 1991; Chappellaz et al, 1990; Mann et al, 1995b; Mann and Lees, 1996; Mommersteeg et al, 1995; Park and Maasch, 1993; Thomson, 1990ab; Yiou et al, 1991;1994;1995;1995) geochemical tracer data (Koch and Mann, 1995), and seismological data (Park et al, 1987; Lees, 1995). Time-frequency ``evolutive'' analyses based on moving window adaptations of MTM have also been applied (e.g., Yiou et al, 1991; Birchfield and Ghil, 1993; Mann et al, 1995b; Mann and Park, 1996b).
MTM, like the method of Blackman and Tukey (1958),
offers the appeal of being nonparametric,
in that it does not prescribe an a priori (e.g., autoregressive)
model for the process generating the time
series under analysis. MTM
attempts to reduce the variance of spectral estimates by
using a small set of tapers (Thomson, 1982, Percival and Walden,1993)
rather than the unique data taper or spectral window used by
Blackman-Tukey methods.
A set of independent estimates of the power spectrum is computed, by
pre-multiplying the data by orthogonal tapers which are
constructed to minimize the spectral leakage due
to the finite length of the data set. The optimal tapers or
``eigentapers'' belong to a family of functions known as
discrete prolate spheroidal sequences (DPSS) and defined as the
eigenvectors of a suitable Rayleigh-Ritz minimization problem, were extensively studied
by Slepian (1978).
Averaging over this (small) ensemble of spectra yields a better and more
stable estimate -- i.e., one with lower variance -- than do single-taper
methods (Thomson, 1990b).
The tapers are the discrete set of eigenfunctions which solve
the variational problem of minimizing leakage outside
of a frequency band of
half bandwidth 
where 
is
the Rayleigh frequency, and p is an integer. Note that the
case p=1 reduces to the trivial Blakman-Tukey case of a single
tapered Discrete Fourier Transform (DFT).
Because the windowing
functions or eigentapers are the specific solution to an
appropriate variational problem, this method is less
heuristic than traditional nonparametric techniques
(see Box and Jenkins, 1970; Jenkins and Watts, 1968).
Detailed algorithms for the calculation of the eigentapers
are readily available (e.g., Thomson, 1990b; Percival
and Walden, 1993)
In practice, only
the first 2p - 1 tapers provide usefully small spectral-leakage
(Slepian, 1978; Thomson, 1982; Park et al, 1987).
Thus, the number of tapers used K should
be less than 2p-1 in any application of MTM.
The choice of the bandwidth 
and number of tapers K thus represents the classical
tradeoff between spectral resolution and the stability or ``variance''
properties of the spectral estimate (Thomson, 1982).
The trivial case K=1 and p=1 is, again, the single-tapered
DFT of Blackman and Tukey.
For typical length instrumental climate records, the
choice K=3, p=2 offers a good compromise between
the required frequency resolution for resolving distinct
climate signals (e.g., ENSO and decadal-scale variability)
and the benefit of multiple spectral degrees of freedom
(see e.g., Mann and Park, 1993).
Longer datasets
can admit the use of a greater number K of tapers while
maintaining a desired frequency resolution, and the optimal
choice of K and p is in general most decidedly
application specific.
MTM can provide estimates of both the singular components (ie,
the ``lines'') and the continuous component (ie, the
background) of the spectrum.
Once the tapers 
are computed for a chosen frequency
bandwidth, the total power spectrum 
can
be estimated by averaging the individual spectra given by each
tapered version of the data set. We
call 
the
kth eigenspectrum, where where 
is the DFT of 
. The
high-resolution multitaper spectrum is a simple weighted
sum of the K eigenspectra,
Its resolution in frequency is 
, which means that ``line'' components will
be detected as peaks or bumps of width . For a white
noise or ``locally white noise'' process (see Thomson, 1982)
the high-resolution
spectrum is chi-squared distributed
with 2K degrees of freedom.
By adjusting the relative weights on the contributions from each of the K eigenspectra, a more leakage-resistant spectral estimate termed the adaptively weighted multitaper spectrum is obtained,
where 
is a weighting function that further guards
against broadband leakage for a non-white (``colored'') but
locally-white process. The adaptive
spectrum estimate has an effective degrees of freedom 
that
generally departs only slightly from the nominal value 2K of
the high-resolution multitaper spectrum.
The purpose of harmonic analysis is to determine the line components-ie the spikes in the spectrum corresponding to a periodic or quasi-periodic signal-in terms of their frequency, amplitude, and phase. The Fourier transform of a clean periodic signal of infinite length yields a Dirac function at the frequency of the signal, viz., a line (or peak of zero width) with infinite magnitude. A spectral estimate based on the methods discussed in earlier sections, gives indirect information on the amplitude of the signal at a given frequency, through the area under the peak centered at that frequency and whose width is, roughly speaking, inversely proportional to the length N of the time series; this area is nearly constant, since the height of the peak is also proportional to N. Harmonic analysis attempts, instead, to determine directly the (finite) amplitude of a (pure) line in the spectrum of a time series of finite length. We explain next how this is done within MTM. Other approaches are described by Macdonald (1989).
Assume the time series X(t) is the sum of a sinusoid of
frequency
and amplitude 
, plus a ``noise'' 
which is
the sum of other sinusoids and white noise. One can then write
If 
are the first K
eigentapers and 
the
DFT of 
, a least-square fit in the frequency domain yields an
estimate 
of the amplitude :
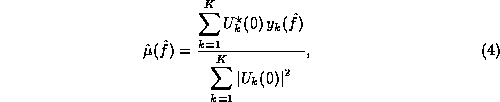
where the asterisk denotes complex conjugation. A statistical confidence interval can be given for the least-squares fit by a Fisher-Snedecor test, or F-test (Kendall and Stuart, 1979). This test is roughly based on the ratio of the variance captured by the filtered portion of the time series X(t), using K eigentapers, to the residual variance. By expanding the variance of the model one finds that it is the sum of two terms,
and
that are respectively the ``explained'' and ``unexplained'' contributions to the variance.
The random variable
would obey a Fisher-Snedecor law with 2 and 2K-2 degrees of freedom if
the time series X(t) were a pure white-noise realization.
One can interpret its numerical value for given data by assuming that
-- i.e., that
X(t) is white- and trying to reject the white noise null hypothesis.
In practice, the spectrum need only be ``locally white'' in the
sense that the K eigenspectra which describe the local characteristics
of the spectrum should be distributed as they would be for white noise
(see Thomson, 1982).
This harmonic-analysis application of MTM is able to detect low-amplitude
harmonic oscillations in a relatively short time series with a high degree of
statistical significance or to
reject
a large amplitude if it failed the F-test, because the
F-value 
does not depend -- to first order -- on the magnitude of
. This feature is an important advantage of MTM over
standard methods where
error bars are essentially
proportional to the amplitude of a peak (e.g., Jenkins and
Wattes, 1968).
However, the implicit assumption in the harmonic-analysis appproach is that
the time series is produced by a process that consists of a
superposition of separate, purely periodic fixed-amplitude components.
If not, a continuous
spectrum (in the case of a colored noise or a chaotic system) will be broken
down into spurious lines with arbitrary frequencies and possibly high
F-values. In essence, the above procedure assumes that ``signals''
are represented by lines in the spectrum corresponding to phase-coherent
harmonic signals, while the ``noise'' is represented by the continuous
component of the spectrum. In geophysical applications, signals are
frequently associated with narrowband, but not strictly harmonic
variability (c.f. the discussion by Park, 1992) and truly harmonic
signals are rarely detected. In such cases, the simple
noise null hypothesis and signal assumptions implicit in the
traditional MTM approach described above loses much of its utility.
The more subtle nature of geophysical signals and noise has led to a more recent generalization of the conventional MTM approach which combines the harmonic signal detection procedure described above, with a criterion for detecting significant narrowband, ``quasi-oscillatory'' signals which may exhibit phase and amplitude modulation, and intermittent oscillatory behavior, but are nonetheless significant relative to some suitably defined null hypothesis (Mann and Lees, 1996). We favour this approach, whichs provides for the detection and significance estimation of both harmonic and anharmonic, narrowband signals in the MTM spectra of time series, making use of a ``robust'' estimate of the background noise. Information from the harmonic peak test of the traditional MTM procedure is retained, but peaks, whether indicated as harmonic or anharmonic, are tested for significance relative to the null hypothesis of a globally red (or, trivially, white) noise background estimated empirically from the data. This is particularly important in climate studies, where the intrinsic inertia of the system leads to greater power (and greater liklihood of prominent peaks in the spectrum) at lower frequencies, even in the absence of any signals (e.g., Hasselmann, 1976). To accomodate the red noise background assumption requisite in geophysical applications, an AR(1) noise process is assumed, although more complex noise models can be motiviated (see the discussion in Mann and Lees, 1996).
The power spectrum of the AR(1) process is given by (e.g., Bartlett, 1966),
for frequency f where 
is the average value of the power spectrum,
related
to the white-noise variance by,
, the Nyquist
frequency, is the highest frequency that can be resolved for
sampling rate 
.
The characteristic noise decay time scale can be
estimated
For periodicities much larger than 
, the spectrum
behavies like a white spectrum.
The approach of Mann and Lees (1996) performs a ``robust''
estimate of the red noise background
by minimizing (as a function of 
)
the misfit between an analytical AR(1) red noise
spectrum and the adaptively weighted multitaper spectrum
convoluted with a median smoother. The median smoothing
operation in the fit insures that the estimated noise
background is
insensitive to outliers (most obviously,
peaks associated with signals) that, properly, should
not influence
the estimation of the global noise background. This
guards against the typical problem of inflated estimates
of noise variance and noise
autocorrelation that arise in a
conventional Box-Jenkins approach due to the contamination
of noise parameters by non-noise contributions (e.g., a
significant trend or oscillatory component of the series).
Mann and Lees (1996)
motivate the choice of a median smoothing width of
as a compromise between
describing the full variation of the background spectrum
over the Nyquist interval, and insensitivity to
narrow spectral features.
Significance levels for harmonic or narrowband spectral features relative to the estimated noise background can be determined from the appropriate quantiles of the chi-squared distribution, approximating the spectrum as being distributed with 2K degrees of freedom (see Mann and Lees, 1996). A reshaped spectrum is determined in which the contributions from harmonic signals are removed (see Thomson, 1982), depending on a significance threshold for the F variance-ratio test described above. In this way, noise background, harmonic, and anharmonic narrowband signals are each independently isolated. The harmonic peak detection procedure provides information as to whether the signals are best approximated as harmonic (phase-coherent sinusoidal oscillations) or narrowband (amplitude and phase modulated, perhaps intermittant oscillations). In either case, they must be significant relative to a specified (e.g., red) noise hypothesis to be isolated as significant.
Once significant peaks have been isolated in the spectrum, relative to the specified null hypothesis, the associated signals can be reconstructed in the time domain using the information from the multitaper decomposition. The signals or ``reconstructed components'' are analagous to those of SSA described in previous sections, except that information from a frequency domain eigendecomposition, rather than a correlation-domain eigendecomposition, is used to reconstruct the detected signal. As in the correlation-domain case, a priori assumptions regarding the domain boundaries must be invoked.
The reconstructed signal corresponding to a peak centered at frequency f0 is written
or, for the discrete case at hand,
where the envelope function A(t) is determined from
a time-domain inversion of the spectral domain information
contained in the K complex eigenspectra (see Park 1992;
Park and Maasch, 1993; Mann and Park, 1994; 1996b).
The envelope A(t) has K complex degrees of freedom,
and allows for phase and amplitude variations in the
time reconstruction of the signal centered
at frequency f0.
The discrete time sequence describing
the complex envelope 
is determined from a discrete
inverse problem using the complex amplitudes
of each of the the K eigenspectra
and appropriate boundary conditions (see Park, 1992;
Park and Maasch, 1993).
The three lowest order boundary contraints in this
inversion involve minimization of the envelope
itself near the boundaries, numerical
mimimization of the slope of the envelope
near the boundaries, or optimization of the smoothness
of the envelope (ie, numerical minimization of the 2nd derivative
near the boundaries).
Any one of these choices might be favoured
if a priori information regarding the characteristics of
the signal is available (see the discussion of Park, 1992).
The amplitude of the seasonal cycle
in surface temperature, for example, is nearly constant in time,
and a minimum slope constraint is most
appropriate for its reconstruction (see Mann and Park, 1996a).
Generally, however, a nearly optimal reconstruction
can always be obtained
through seeking
the weighted linear combination of these 3 contraints that minimizes
the mean-square misfit of the reconstructed signal with
respect to the raw data series (Mann and Park, 1996b).
We favour this method of time-domain inversion.
|
|
|
|
|