Stochastic Lattice Model

MOTIVATION

This project is inspired by the concept of multiple equilibria or multiple regimes of behavior in the climate system (Ghil and Childress, 1987), combined with the concept of emergent behavior in lattice models (Anderson, 1997).  These two concepts are applied to a lattice of single-column mixed-layer models. An important application would be to resolve the variability of stratocumulus cloud fractions, in observations and GCMs.

The Mixed Layer Model (MLM) of Lilly (1968) has, for almost 40 years, been a useful tool to study dry and moist atmospheric boundary layers. Randall and Suarez (1984) showed it to possess multiple equilibria. We reproduce this with our MLM (Stevens 2002; Zhang et al., 2005) in the bifurcation diagram of Figure 1, which plots mixed-layer height H vs. large-scale divergence D.  The two solid lines represent the two branches of the stable steady states: the shallow, warm and moist clear sky boundary layer (CSBL) versus vs. the deep cool and dry stratocumulus-topped boundary layer (STBL); the dashed line represents  the branch of intermediate, unstable solutions. 

The behavior shown in Figure 1 is also found in the heat and moisture fields of the model, with respect to other control parameters, besides D, such as sea surface temperature (SST), wind speed, free troposphere temperature and moisture and cloud top radiative driving.  This fairly robust model behavior suggests that regime transitions between CSBL and STBL state are possible when the system is subject to various fluctuations, which may accumulate to overcome the potential barrier associated with the presence of the unstable equilibrium.  Such fluctuations could arise either internally, form small-, cloud-scale effects or externally, from large-, synoptic-scale variability in the model's  control parameter fields. 

This observation inspires us to formulate a stochastic-perturbation model to simulate such fluctuations.  A possible transition is shown in Figure 2, where LWP stands for liquid water path.  

Stratocumulus interests us because of its cooling effect on the global energy balance and subsequent feedbacks on  climate and synoptic dynamics.  To resolve its cloud fraction becomes more and more demanding.   The cloud morphology of open cells (cloud-free air cells with cloudy air on the edge) and closed cells (cloudy air cells with cloud-free air on the edge) hints not only independent local convection or subsidence but also connections, besides advections, between the neighboring cells.  The observations on the pockets of open cells (POCs) during DYCOMSII by Stevens et al (2005) support the idea that drizzle promotes regional cloud transitions.              

This hints us, while the local dynamics are represented by MLM, an interaction rule can be specified based on the drizzle effect.

                
         
      Figure 1.  Multiple Equilibria in Mixed Layer Model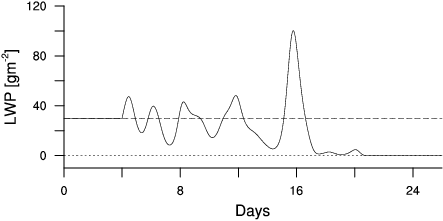
       
         
        Figure 2. Regime transit from  STBL  to  CSBL


     Figure 3. Pocket of Open Cells (POCs, DYCOMSII)
  PRELIMINARY WORK (2005)

MODEL OVERVIEW
         
         
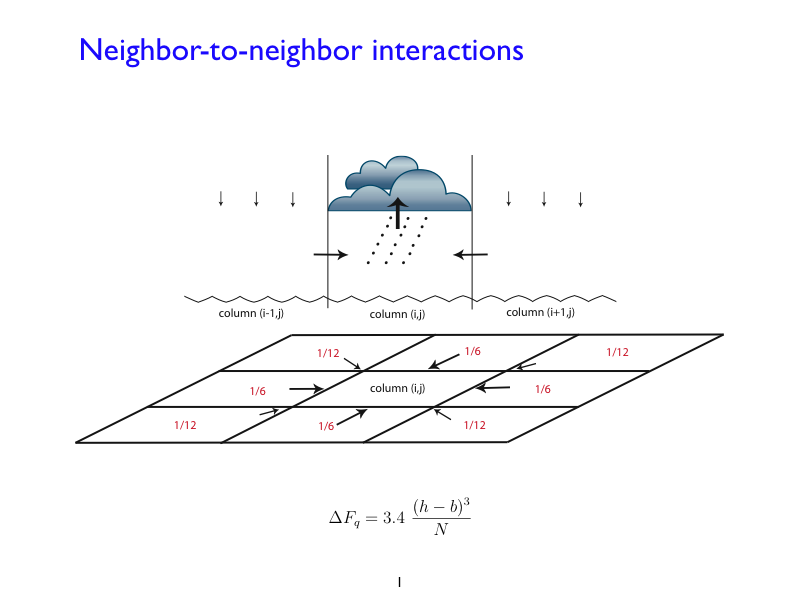
           Figure 4.  The lattice model (PDF)                                                         Figure 5. The illustration of the interactions (PDF)
  • Different components in Figure 4.: "M" stands for mixed-layer physics; "I" stands for interactions between neighboring sites; "S" stands for contributions from stochastic fluctuations in divergence fields. 
  • Physics component "M" is based on mixed-layer model physics. Entrainment is driven by both surface windsheer and buoyancy.  Cloud-top radiative cooling is coupled to LWP.  Drizzle is parameterized based on van Zanten et al (2005).
  • About advection component.  Right now, we have 4 choices, min-mod, superbee, mc (monotonized centered), and van Leer. All of them seem to produce more diffusion than we expect.   This is seen in the following simple model runs. However noise and interaction components have much more priority than this one, so right now we just choose to leave it behind.
  • Noise component "S".   Based on analysis of divergence (PNG PDF) derived from ECMWF Reanalysis data, an autoregressive model (PNG PDF) is constructed for the divergence field.   With no interactions, the equilbrium cloud fraction for a local site is shown to be a function (PNG, PDF) of the noise model parameters: the mean divergence, the noise level and the autocorrelation timescale.  White Gaussian noise (WGN) is generated by Box-Muller method (Polar method, Ross, 1988).  Right now noise is only given to mass field (h).
  • Interaction component "I".  An eight nearest-neighbor interaction rule (PNG PDF) is construceted based on mass and energy conservation law and is illustrated in Figure 5.  The interaction is mainly promoted by drizzle process.  On one hand drizzle tends  to inhibit entrainment, lower cloud top and thin cloud layer; on the other hand it induces convergence and divergence in the neighbors.  The local enhancement of mass is balanced by nearest 8 neighboring sites, therefore energy and moisture are exchanged.

RESULT
Terminology:
  • control-run: with no interactions nor stochastic component
  • inter-run: with interactions only
  • noise-run: with stochastic component only
  • both-run: with both interactions and stochastic component
  • contour figures show the liquid water depth field (g/m^2)
Case Studies
  • Case 1: random initial cloud depth
    • overview (PNG PDF)
    • analysis
      • difference between control-run and inter-run (PNG PDF)
      • difference between noise-run and both-run   (PNG PDF)
      • cloud fraction evolution and bifurcation diagram (PNG PDF)
  • Case 2: random droplet number density
    • overview (PNG PDF)
    • analysis
      • difference between control-run and inter-run (PNG PDF)
      • difference between noise-run and both-run   (PNG PDF)
      • cloud fraction evolution and bifurcation diagram (PNG PDF)

REFERENCE
  • Anderson, P. W., 1997: Basic Notions of Condensed Matter Physics.  Perseus Publishing.  564pp
  • Ghi, M. and S. Childress, 1987: Topics in Geophysics Fluid Dynamics: Atmospheric Dynamics, Dynamo Theory and Climate Dynamics.  Springer-Verlag, New York/Berlin/London/Paris/Tokyo.  485pp
  • Lilly, D. K., 1968: Models of cloud topped mixed layers under a strong inversion.  Quart. J. Roy. Meteor. Soc., 94, 292-309.
  • Lin, J. W.-B. and J. D. Neelin, 2002: Considerations for stochastic convective parameterization.  J. Atmos. Sci., 59, 959-975.
  • Randall, D. A. and M. J. Suarez, 1984: On the dynamics of stratocumulus formation and dissipation.  J. Atmos. Sci., 41, 3052-3057.
  • Stevens, B., 2002: Entrainment in stratocumulus mixed layers.  Quart. J. Roy. Meteor. Soc., 128, 2663-2690.
  • Stevens, B., Y. Zhang, and M. Ghil, 2005: Stochastic effects in the representation of stratocumulus-topped mixed layers. Proc. ECMWF Workshop on Representation of Sub-grid Processes Using Stochastic-Dynamic Models, June 2005, Shinfield Park, Reading, UK, pp. 79--90.
  • Stevens, B. and co-authors, 2005: Pockets of open cells (pocs) and drizzle in marine stratocumulus.  Bull. Amer. Meteor. Soc., 86, 51-57.
  • Van Zanten, M. C. and B. Stevens, 2005: On the observed structure of heavily precipitating marine stratocumulus. J. Atmos. Sci., 62, 4327-4342
  • Zhang, Y., B. Stevens, and M. Ghil, 2005: On the Diurnal Cycle and Susceptibility to Aerosol Concentration in a Stratocumulus-Topped Mixed Layer. Quart. J. Roy. Meteorol. Soc., 131, 1567--1584.